
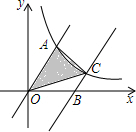
 如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6.
如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6. 分析 根据等底同高的三角形的面积相等,得出△OAB的面积是3$\sqrt{3}$,进而求得AD的长,得出A的纵坐标,代入y=2x,即可求得横坐标,代入反比例函数解析式即可求得k的值.
解答  解:连接AB,作AD⊥OB于D,
解:连接AB,作AD⊥OB于D,
∵OA∥BC,
∴△AOC和△AOB是等底同高,
∴S△AOB=S△OAC=3$\sqrt{3}$,
∵B(3,0),
∴OB=3,
∴$\frac{1}{2}$OB•AD=3$\sqrt{3}$,
∴AD=2$\sqrt{3}$,
把y=2$\sqrt{3}$代入y=2x得,x=$\sqrt{3}$,
∴A($\sqrt{3}$,2$\sqrt{3}$),
∴k=2$\sqrt{3}$×$\sqrt{3}$=6.
故答案为6.
点评 本题是反比例函数与三角形的面积的综合计算题,根据等底同高的三角形的面积相等求得A的纵坐标是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
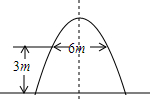 蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m)
蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,点D在⊙O上,BD=BA,∠DAC=2∠ABC,⊙O交BC于点E,AD交BC于点F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,点D在⊙O上,BD=BA,∠DAC=2∠ABC,⊙O交BC于点E,AD交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com