
【题目】如图所示,在△![]() 中,
中,![]() >
>![]() ,
,![]() ∥
∥![]() =
=![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,则添加下列哪一个条件后,仍无法判定△
,则添加下列哪一个条件后,仍无法判定△![]() 与△
与△![]() 全等( )
全等( )

A. ![]() ∥
∥![]() B.
B. ![]() C. ∠
C. ∠![]() =∠
=∠![]() D. ∠
D. ∠![]() =∠
=∠![]()
【答案】C
【解析】
根据平行线的性质得到∠BDF=∠EFD,根据DE∥BC,![]() =
=![]() 得到∠EDF=∠BFD,根据全等三角形的判定即可判断A;由
得到∠EDF=∠BFD,根据全等三角形的判定即可判断A;由![]() =
=![]() =BF,∠EDF=∠BFD,DF=DF即可得到△BFD≌△EDF;由∠A=∠DFE,证不出△BFD≌△EDF;由∠B=∠DEF,∠EDF=∠BFD,DF=DF,得到△BFD≌△EDF.
=BF,∠EDF=∠BFD,DF=DF即可得到△BFD≌△EDF;由∠A=∠DFE,证不出△BFD≌△EDF;由∠B=∠DEF,∠EDF=∠BFD,DF=DF,得到△BFD≌△EDF.
A.∵EF∥AB,
∴∠BDF=∠EFD,
∵![]() =
=![]() ,DE∥BC,
,DE∥BC,
∴∠EDF=∠BFD(平行线的性质),
∵DF=DF,
∴△BFD≌△EDF,故本选项正确;
B.∵![]() =
=![]() =BF,∠EDF=∠BFD,DF=DF,∴△BFD≌△EDF,故本选项正确;
=BF,∠EDF=∠BFD,DF=DF,∴△BFD≌△EDF,故本选项正确;
C. 由∠A=∠DFE,证不出△BFD≌△EDF,故本选项错误;
D.∵∠B=∠DEF,∠EDF=∠BFD,DF=DF,∴△BFD≌△EDF(AAS),故本选项正确.
故选:C.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一单杆高2.2m,两立柱之间的距离为1.6m,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状. 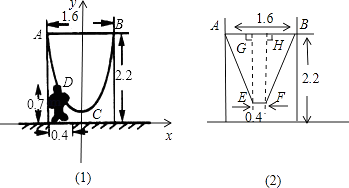
(1)一身高0.7m的小孩站在离立柱0.4m处,其头部刚好触上绳子,求绳子最低点到地面的距离;
(2)为供孩子们打秋千,把绳子剪断后,中间系上一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,求这时木板到地面的距离.(供选用数据: ![]() ≈1.8,
≈1.8, ![]() ≈1.9,
≈1.9, ![]() ≈2.1)
≈2.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D. 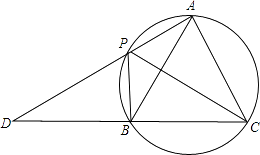
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)+( ![]() m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在海上观察所A,我边防海警发现正北5km的B处有一可疑船只正在向东方向12km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为60km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?

查看答案和解析>>
科目:初中数学 来源: 题型:
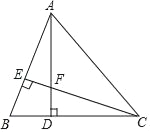
【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
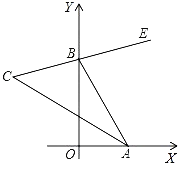
【题目】如图,在直角坐标系中,点A,B分别在射线Ox,Oy上移动,BE是∠ABy的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否为定值?请给出证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com