
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.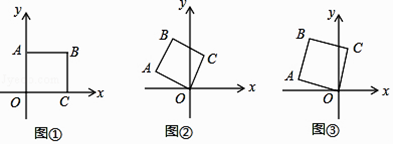
【答案】解:(Ⅰ)过点A作x轴的垂线,垂足为D,∠ADO=90°, 
∵旋转角为60°,
∴∠AOD=90°﹣60°=30°,
∴AD= ![]() AO=1,DO=
AO=1,DO= ![]() ,
,
∴A(﹣ ![]() ,1);
,1);
(Ⅱ)连接BO,过B作BD⊥y轴于D,
∵旋转角为75°,∠AOB=45°,
∴∠BOD=75°﹣45°=30°,
∵∠A=90°,AB=AO=2,
∴BO=2 ![]() ,
,
∴Rt△BOD中,BD= ![]() ,OD=
,OD= ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ).
).
【解析】(1)过点A作x轴的垂线,垂足为D,∠ADO=90°,根据旋转角得出∠AOD=30°,进而得到AD= ![]() AO=1,DO=
AO=1,DO= ![]() ,据此可得点A的坐标;(2)连接BO,过B作BD⊥y轴于D,根据旋转角为75°,可得∠BOD=30°,根据勾股定理可得BO=2
,据此可得点A的坐标;(2)连接BO,过B作BD⊥y轴于D,根据旋转角为75°,可得∠BOD=30°,根据勾股定理可得BO=2 ![]() ,再根据Rt△BOD中,BD=
,再根据Rt△BOD中,BD= ![]() ,OD=
,OD= ![]() ,可得点B的坐标.
,可得点B的坐标.
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】根据题意解答 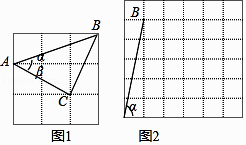
(1)如图1,如果ɑ,β都为锐角,且tanɑ= ![]() ,tanβ=
,tanβ= ![]() ,则ɑ+β=;
,则ɑ+β=;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
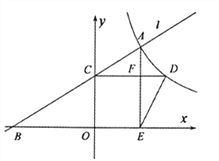
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
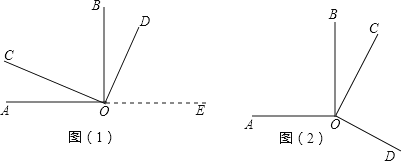
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0
(1)求点C表示的数:
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动
(i)当P、Q两点在数轴上D点相遇时,求此时C、D两点之间的距离;
(ii),若AP+BQ=2PQ,求时间t.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图像如图所示,则下列结论:
①abc>0;②a+b+c=2;③b>1;④a< ![]() .
.
其中正确的结论是( )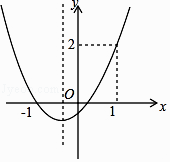
A.①②
B.②③
C.③④
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
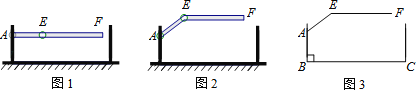
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com