
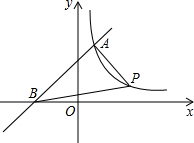
 如图,一次函数y=x+3与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(m,4),与x轴相交于点B.
如图,一次函数y=x+3与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(m,4),与x轴相交于点B.分析 (1)由点A在一次函数解析式中,可得出关于m的一元一次方程,解方程可求出m的值,从而得出点A的坐标,由点A的坐标结合反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数的解析式;
(2)设点P的坐标为(m,n),根据反比例函数图象上点的坐标特征以及两直线垂直斜率乘积为-1,可得出关于m、n的二元一次方程组,解方程组即可得出结论.
解答 解:(1)∵点A(m,4)在一次函数y=x+3图象上,
∴4=m+3,解得:m=1,
∴点A的坐标为(1,4).
∵A(1,4)在反比例函数$y=\frac{k}{x}$图象上,
∴k=1×4=4.
∴反比例函数的解析式为$y=\frac{4}{x}$.
(2)设点P的坐标为(m,n),
由题意得:$\left\{\begin{array}{l}{mn=4}\\{\frac{n-4}{m-1}×1=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1}\\{n=4}\end{array}\right.$(舍去),或$\left\{\begin{array}{l}{m=4}\\{n=1}\end{array}\right.$,
∴点P的坐标为(4,1).
故答案为:(4,1).
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及垂线的性质,解题的关键是:(1)求出点A的坐标;(2)找出关于m、n的二元一次方程组.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,根据反比例函数图象上点的坐标特征求出反比例函数的系数k是关键.


科目:初中数学 来源: 题型:解答题
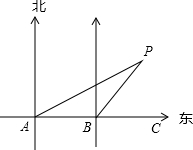 海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.
海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
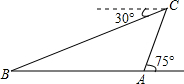 为了加快我省城乡公路建设,我省计划“十三五”期间高速公路运营里程达1000公里,进一步打造城乡快速连接通道,某地计划修建一条高速公路,需在小山东西两侧A,B之间开通一条隧道,工程技术人员乘坐热气球对小山两侧A、B之间的距离进行了测量,他们从A处乘坐热气球出发,由于受西风的影响,热气球以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为多少米?
为了加快我省城乡公路建设,我省计划“十三五”期间高速公路运营里程达1000公里,进一步打造城乡快速连接通道,某地计划修建一条高速公路,需在小山东西两侧A,B之间开通一条隧道,工程技术人员乘坐热气球对小山两侧A、B之间的距离进行了测量,他们从A处乘坐热气球出发,由于受西风的影响,热气球以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com