

 △ACD是等腰三角形,∠D
△ACD是等腰三角形,∠D =30°.
=30°.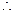 ∠CAD=∠CDA=30°.
∠CAD=∠CDA=30°. AO=CO,
AO=CO,
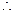 △AOC是等腰三角形.…………………
△AOC是等腰三角形.………………… ……2分
……2分 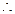 ∠CAO=∠ACO=30°,
∠CAO=∠ACO=30°,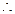 ∠COD=60°.…………………………………3分
∠COD=60°.…………………………………3分 ∠CDO=30°,
∠CDO=30°,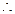 ∠DCO=90°.………………………………4分
∠DCO=90°.………………………………4分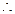 CD是⊙O的切线,即直线CD与⊙O相切.……………………………5分
CD是⊙O的切线,即直线CD与⊙O相切.……………………………5分 . ………………………………6分
. ………………………………6分 ∠CDO=30°,
∠CDO=30°,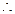 OD=2OC=10. AD=AO+OD=15……………………………………………7分
OD=2OC=10. AD=AO+OD=15……………………………………………7分 ∠EDA=30°,
∠EDA=30°,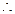 点A到CD边的距离为:
点A到CD边的距离为: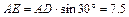 .…………………………9分
.…………………………9分

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源:不详 题型:填空题
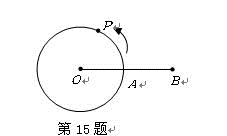
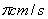 的速度沿圆周逆时针运动,当点P回到点A就停止运动.当点P运动的时间为 s时,BP与⊙O相切.
的速度沿圆周逆时针运动,当点P回到点A就停止运动.当点P运动的时间为 s时,BP与⊙O相切.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.100π | B.200π | C.300π | D.400π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com