
 如图是两个重叠的直角三角形,将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形,求阴影部分的面积(单位:厘米)
如图是两个重叠的直角三角形,将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形,求阴影部分的面积(单位:厘米) 分析 先根据图形平移的性质得出△ABC≌△DEF,故图中阴影部分的面积与梯形ABEH的面积相等,根据梯形的面积公式即可得出结论.
解答 解:∵△DEF由△ABC平移而成,
∴△ABC≌△DEF,
∴图中阴影部分的面积与梯形ABEH的面积相等,
∵AB=8厘米,DH=3厘米,
∴EH=DE-DH=AB-DH=8-3=5(厘米),
∵BE=5厘米,
∴S阴影=S梯形ABEH=$\frac{1}{2}$(EH+AB)•BE=$\frac{1}{2}$×(5+8)×5=32.5(平方厘米).
答:阴影部分的面积是32.5平方厘米.
点评 本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
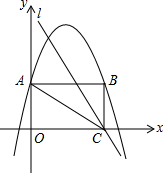 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C分别在y轴、x轴上,点B在第一象限,抛物线y=-$\frac{1}{2}{x}^{2}$+4x+6经过A、B两点.
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C分别在y轴、x轴上,点B在第一象限,抛物线y=-$\frac{1}{2}{x}^{2}$+4x+6经过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在⊙O1中,AB为直径,AB=4,点C在⊙O1上,连接AC,以AC为直径作⊙O2,⊙O1在⊙O2的内部,⊙O2的面积为3π,点D在AB上运动,当线段CD的长度最短时,AD的长度为( )
如图,在⊙O1中,AB为直径,AB=4,点C在⊙O1上,连接AC,以AC为直径作⊙O2,⊙O1在⊙O2的内部,⊙O2的面积为3π,点D在AB上运动,当线段CD的长度最短时,AD的长度为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com