
分析 利用尺规作图画出图形即可.作CM⊥OB于M,CN⊥OA于N,AE⊥OB于E.首先证明BC:AC=3:2,利用勾股定理求出AB,AC,设CN=x,则OC=2x,ON=$\sqrt{3}$x,在Rt△CNA中,根据AC2=CN2+AN2,列出方程即可解决问题.
解答 解:图形如图所示,作CM⊥OB于M,CN⊥OA于N,AE⊥OB于E.
∵OC平分∠AOB,
∴CM=CN,
∵$\frac{{S}_{△BOC}}{{S}_{△AOC}}$=$\frac{\frac{1}{2}OB•CM}{\frac{1}{2}OA•CN}$=$\frac{BC}{CA}$,
∵OA=20,OB=30,
∴$\frac{BC}{AC}$=$\frac{3}{2}$,
在Rt△AOE中,∵OA=20,∠AOE=60°,
∴∠OAE=30°,
∴OE=10,BE=20,AE=10$\sqrt{3}$,
在Rt△AEB中,AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=10$\sqrt{7}$,
∴AC=$\frac{2}{5}$AB=4$\sqrt{7}$,
设CN=x,则OC=2x,ON=$\sqrt{3}$x,
在Rt△CNA中,∵AC2=CN2+AN2,
∴x2+(20-$\sqrt{3}$x)2=(4$\sqrt{7}$)2,
解得x=6$\sqrt{3}$或4$\sqrt{3}$(舍弃),
∴OC=12$\sqrt{3}$,
∴AC:OC=4$\sqrt{7}$:12$\sqrt{3}$=$\sqrt{21}$:9.
点评 本题考查作图-基本作图、勾股定理、角平分线的性质定理等知识,解题的关键是利用面积法证明BC:AC=3:2,学会利用参数,把问题转化为方程解决,属于中考常考题型.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
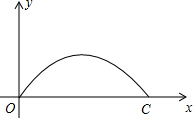 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.
如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,∠A=90°,
在Rt△ABC中,∠A=90°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
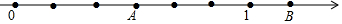
| A. | $1\frac{1}{3}$ | B. | $1\frac{1}{4}$ | C. | $1\frac{1}{5}$ | D. | $1\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com