

分析 (1)只需求出点P的坐标,然后用两点间的距离公式就可求出PD-PC的值;
(2)由题可得点P(x,$\frac{2}{x}$),然后运用两点间的距离公式可得PD=|x+$\frac{2}{x}$+2|,PC=|x+$\frac{2}{x}$-2|.由x>0可推出x+$\frac{2}{x}$+2>0,x+$\frac{2}{x}$-2>0,从而可求出PD-PC的值;
(3)设直线PE的解析式为y=kx+b,由点C(2,2)在直线PE上可得b=2-2k,即得直线PE的解析式为y=kx+2-2k,则x1、x2是方程kx+2-2k=$\frac{2}{x}$即kx2+(2-2k)x-2=0的两根,然后结合条件PE=4,运用两点间的距离公式和根与系数的关系求出k的值,代入方程kx2+(2-2k)x-2=0,解这个方程就可得到点P的坐标.
解答 解:(1)∵点P(1,m)为双曲线y=$\frac{2}{x}$上一点,
∴m=2,P(1,2).
∵C(2,2)、D(-2,-2),
∴PD=$\sqrt{(-2-1)^{2}+(-2-2)^{2}}$=5,
PC=$\sqrt{(2-1)^{2}+(2-2)^{2}}$=1,
∴PD-PC=5-1=4;
(2)PD-PC的值是定值4.
理由:∵点P(x,y)(x>0)为双曲线y=$\frac{2}{x}$上一动点,
∴y=$\frac{2}{x}$,P(x,$\frac{2}{x}$),
∴PD=$\sqrt{(x+2)^{2}+(\frac{2}{x}+2)^{2}}$=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}+4x+\frac{8}{x}+8}$
=$\sqrt{(x+\frac{2}{x})^{2}+4(x+\frac{2}{x})+4}$=$\sqrt{(x+\frac{2}{x}+2)^{2}}$=|x+$\frac{2}{x}$+2|.
同理PC=|x+$\frac{2}{x}$-2|.
∵x>0,∴$\frac{2}{x}$>0,
∴x+$\frac{2}{x}$+2>0,x+$\frac{2}{x}$≥2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$,
∴x+$\frac{2}{x}$-2>0,
∴PD-PC=(x+$\frac{2}{x}$+2)-(x+$\frac{2}{x}$-2)=4;
(3)设直线PE的解析式为y=kx+b,
∵点C(2,2)在直线PE上,
∴2k+b=2,
∴b=2-2k,
∴直线PE的解析式为y=kx+2-2k,
设x1、x2是方程kx+2-2k=$\frac{2}{x}$即kx2+(2-2k)x-2=0的两根,
则有x1+x2=$\frac{2k-2}{k}$=2-$\frac{2}{k}$,x1•x2=-$\frac{2}{k}$,
∴(x1-x2)2=(x1+x2)2-4x1•x2=(2-$\frac{2}{k}$)2-4(-$\frac{2}{k}$)=4+$\frac{4}{{k}^{2}}$,
∴PE2=(x1-x2)2+($\frac{2}{{x}_{1}}$-$\frac{2}{{x}_{2}}$)2=(x1-x2)2+4•$\frac{({x}_{1}-{x}_{2})^{2}}{({x}_{1}•{x}_{2})^{2}}$
=(4+$\frac{4}{{k}^{2}}$)+4•$\frac{4+\frac{4}{{k}^{2}}}{\frac{4}{{k}^{2}}}$=4+$\frac{4}{{k}^{2}}$+4k2+4=$\frac{4}{{k}^{2}}$+4k2+8.
∵PE=4,∴$\frac{4}{{k}^{2}}$+4k2+8=16,
∴$\frac{4}{{k}^{2}}$+4k2-8=0,
整理得(k2-1)2=0,
解得k1=1,k2=-1.
由条件“延长PC交双曲线另一点E”可得k<0,
∴k=-1,
代入kx2+(2-2k)x-2=0得,
-x2+4x-2=0,
解得x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
当x=2+$\sqrt{2}$时,$\frac{2}{x}$=$\frac{2}{2+\sqrt{2}}$=2-$\sqrt{2}$,点P(2+$\sqrt{2}$,2-$\sqrt{2}$).
当x=2-$\sqrt{2}$时,$\frac{2}{x}$=$\frac{2}{2-\sqrt{2}}$=2+$\sqrt{2}$,点P(2-$\sqrt{2}$,2+$\sqrt{2}$).
∴点P的坐标为(2+$\sqrt{2}$,2-$\sqrt{2}$)或(2-$\sqrt{2}$,2+$\sqrt{2}$).
点评 本题主要考查了直线与双曲线的交点问题、双曲线上点的坐标特征、两点间的距离公式、根与系数的关系、解高次方程等知识,将根号内的代数式配成完全平方是解决第(2)小题的关键,将两点间的距离公式与根与系数的关系相结合是解决第(3)小题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
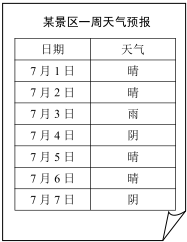 某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一次骰子,在骰子向上的一面上的点数大于0 | |
| B. | 掷一次骰子,在骰子向上的一面上的点数为7 | |
| C. | 掷三次骰子,在骰子向上的一面上的点数之和刚好为18 | |
| D. | 掷两次骰子,在骰子向上的一面上的点数之积刚好是11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
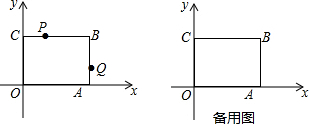
 如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
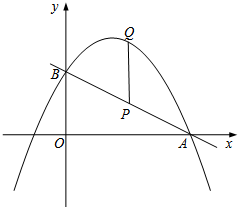 如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com