

���� ��1�����ݵȱ������ε����ʵõ�BC=CE��OC=CD����OCD=��BCE=60�㣬��á�OCB=��DCE������ȫ�������ε����ʼ��ɵõ����ۣ�
��2�����ɵ�B��0��6�����õ�OB=6������ȫ�������ε����ʵõ���CDE=��BOC=90�㣬���ݵȱ������ε����ʵõ���DEC=30�㣬���CE=4$\sqrt{3}$����E��EF��x����F���������μ��ɵõ����ۣ��ڴ��ڣ���ͼd����CE=CP=4$\sqrt{3}$ʱ����CE=PE�����ݵ��������ε����ʼ��ɵõ����ۣ��۲���仯����ͼc������EM�����������ε������ʽ���ɵõ����ۣ�
��� �⣺��1���ߡ�ODC�͡�EBC���ǵȱ������Σ�
��BC=CE��OC=CD����OCD=��BCE=60�㣬
���OCB=��DCE��
�ڡ�BCO���ECD�У�$\left\{\begin{array}{l}{BC=CE}\\{��OCB=��DCE}\\{OC=CD}\end{array}\right.$��
���BCO�ա�ECD��
��BC=CE��
��2���١ߵ�B��0��6����
��OB=6��
�ɣ�1��֪��BCO�ա�ECD��
���CDE=��BOC=90�㣬
��DE��BC��
�ߡ�EBC�ǵȱ������Σ�
���DEC=30�㣬
���OBC=��DEC=30�㣬
��OC=$\frac{\sqrt{3}}{3}$OB=2$\sqrt{3}$��BC=4$\sqrt{3}$��
��CE=4$\sqrt{3}$��
��E��EF��x����F��
�ߡ�DCO=��BCE=60�㣬
���ECF=60�㣬
��CE=BC=4$\sqrt{3}$��
��CF=2$\sqrt{3}$��EF=$\frac{\sqrt{3}}{2}$CE=6��
��E��4$\sqrt{3}$��6����
�ڴ��ڣ���ͼd����CE=CP=4$\sqrt{3}$ʱ��
��OC=2$\sqrt{3}$��
��OP1=2$\sqrt{3}$��OP2=6$\sqrt{3}$��
��P1��-2$\sqrt{3}$��0����P2��6$\sqrt{3}$��0����
��CE=PE��
�ߡ�ECP=60�㣬
���CPE�ǵȱ������Σ�
��P2��P3�غϣ�
�൱��PECΪ����������ʱ��P��-2$\sqrt{3}$��0������6$\sqrt{3}$��0����
�۲���仯����ͼc������EM��
��S��BCE=$\frac{1}{2}$BC•DE=$\frac{1}{2}$BE•GM+$\frac{1}{2}$CE•MN��
��BC=CE=BE��
��GM+MN=DE=6��
��MN+MG��ֵ���ᷢ���仯��
���� ���⿼����ȫ�������ε��ж������ʣ��ȱ������ε��ж������ʣ����������ε��ж�������������ļ��㣬�������յȱ������ε������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-��x-2��2-1 | B�� | y=-��x-2��2+1 | C�� | y=-��x+2��2+1 | D�� | y=-��x+2��2-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ��߳�Ϊ12��������ֽƬABCD�Ķ���A�۵���DC���ϵĵ�E��ʹDE=5���ۺ�ΪPQ����PQ�ij�Ϊ13��
��ͼ����һ��߳�Ϊ12��������ֽƬABCD�Ķ���A�۵���DC���ϵĵ�E��ʹDE=5���ۺ�ΪPQ����PQ�ij�Ϊ13���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ���BE=DF������EAF=30�㣬��sin��EDF=$\frac{��\sqrt{3}-1��\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$��
��ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ���BE=DF������EAF=30�㣬��sin��EDF=$\frac{��\sqrt{3}-1��\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
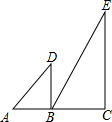 ��ͼ����ֱ��AC��ͬ����Rt��ABD��Rt��BCE����֪��ABD=��C=90�㣬��A=45�㣬��E=30�㣬������ABD�Ƶ�B��˳ʱ�뷽����ת����AD��BCʱ����ת�ĽǶ��ǣ�������
��ͼ����ֱ��AC��ͬ����Rt��ABD��Rt��BCE����֪��ABD=��C=90�㣬��A=45�㣬��E=30�㣬������ABD�Ƶ�B��˳ʱ�뷽����ת����AD��BCʱ����ת�ĽǶ��ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1����x��0 | B�� | x��1 | C�� | x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com