
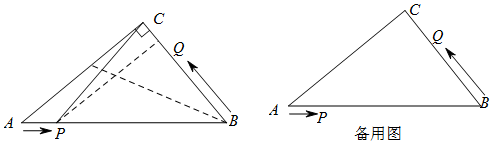
分析 (1)分两种情形讨论求解①当AP=PB时,可以证明PA=PC.②当AC=AP时;
(2)当点Q在边BC上运动时,过点Q作QH⊥AB于H,由△QHB∽△ACB,推出$\frac{QH}{AC}$=$\frac{QB}{AB}$,可得QH=$\frac{8}{5}$xcm,根据y=$\frac{1}{2}$BP•QH,列出式子即可;
(3)存在.如图作QH⊥AB于H.由S△PBQ:S四边形APQC=5:3,可得-$\frac{4}{5}$x2+8x=$\frac{5}{8}$×$\frac{1}{2}$×6×8,解方程即可解决问题;
(4)存在.如图作QH⊥AB于H.首先证明QC=QH=2t-6,由△AQH∽△ABC,可得$\frac{AQ}{AB}$=$\frac{QH}{BC}$,推出$\frac{14-2t}{10}$=$\frac{2t-6}{6}$,解方程即可解决问题;
解答 解:(1)①当AP=PB时,∵∠ACB=90°,
∴CP=PA=PB,
∴t=5,
②当AC=AP时,t=8,
∴t=5s或8s时,△APC是等腰三角形.
(2)当点Q在边BC上运动时,过点Q作QH⊥AB于H,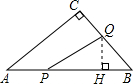
∵AP=xcm,
∴BP=(10-x)cm,BQ=2xcm,
∵△QHB∽△ACB,
∴$\frac{QH}{AC}$=$\frac{QB}{AB}$,
∴QH=$\frac{8}{5}$xcm,
y=$\frac{1}{2}$BP•QH=$\frac{1}{2}$(10-x)•$\frac{8}{5}$x=-$\frac{4}{5}$x2+8x(0<x≤3).
(3)存在.∵S△PBQ:S四边形APQC=5:3,
∴-$\frac{4}{5}$x2+8x=$\frac{5}{8}$×$\frac{1}{2}$×6×8,
解得x=$\frac{15}{2}$或$\frac{5}{2}$,
∴t=$\frac{15}{2}$s或$\frac{5}{2}$s时,S△PBQ:S四边形APQC=5:3.
(4)存在.如图作QH⊥AB于H.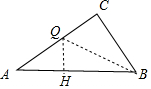
∵∠QBC=∠QBA,QC⊥BC,QH⊥AB,
∴QC=QH=2t-6,AQ=14-2t,
∵∠A=∠A,∠AHQ=∠C=90°,
∴△AQH∽△ABC,
∴$\frac{AQ}{AB}$=$\frac{QH}{BC}$,
∴$\frac{14-2t}{10}$=$\frac{2t-6}{6}$,
∴t=$\frac{9}{2}$,
∴t=$\frac{9}{2}$s时,BQ平分∠ABC.
点评 本题考查四边形综合题、定义是矩形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
 Rt△ABC中,∠ACB=90°,直线DE过C点,且有DE∥AB,若∠1=65°,则∠2的度数是( )
Rt△ABC中,∠ACB=90°,直线DE过C点,且有DE∥AB,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届山东泰安市中考二模数学试卷(解析版) 题型:解答题
我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2017届山东泰安市中考二模数学试卷(解析版) 题型:填空题
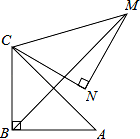
如图,在 Rt△ABC 中,∠ABC=90°,AB=BC=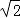 ,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .
,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .
查看答案和解析>>
科目:初中数学 来源:2017届广东省揭阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
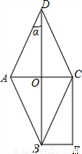
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是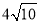 ,
, 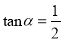 ,求四边形OBEC的面积。
,求四边形OBEC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com