ЗжЮіЃКЃЈ1ЃЉЯШЧѓГіBЕузјБъЃЌДњШыХзЮяЯпy=ax
2ЃЈaЃМ0ЃЉЕУaЕФжЕЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌПЩжЄЁїAEOЁзЁїOFBЃЌЕУГіAE=2OEЃЌПЩЕУЗНГЬЕуAЕФКсзјБъЃЎ
ЃЈ3ЃЉЩшAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ
-n2ЃЉЃЈnЃО0ЃЉЃЌвзжЊЁїAEOЁзЁїOFBЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩжЊНЛЕуAЁЂBЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЈ0ЃЌ-2ЃЉЃЎ
НтД№ЃК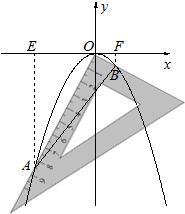
НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ
Ёп
OA=OB=2ЃЌЁЯAOB=90ЁуЃЌ
ЁрAC=OC=BC=2ЃЌ
ЁрBЃЈ2ЃЌ-2ЃЉЃЌ
НЋBЃЈ2ЃЌ-2ЃЉДњШыХзЮяЯпy=ax
2ЃЈaЃМ0ЃЉЕУЃЌ
a=-ЃЎ
ЃЈ2ЃЉНтЗЈвЛЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ
-ЃЉЃЌ
Ёр
BF=ЃЎ
гжЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
гжЁпЁЯAEO=ЁЯOFB=90ЁуЃЌ
ЁрЁїAEOЁзЁїOFBЃЌ
Ёр
===2ЃЌ
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌдђOE=mЃЌ
AE=m2ЃЌ
Ёр
m2=2mЃЌ
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈЖўЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ
-ЃЉЃЌ
Ёр
tanЁЯOBF===2ЃЌ
ЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
Ёр
=tanЁЯAOE=tanЁЯOBF=2ЃЌ
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌ
дђOE=mЃЌ
AE=m2ЃЌ
Ёр
m2=2mЃЌ
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈШ§ЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ
-ЃЉЃЌ
ЩшAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌ
дђ
OB2=12+()2=ЃЌ
OA2=m2+m4ЃЌ
AB2=(1+m)2+(-+m2)2ЃЌ
ЁпЁЯAOB=90Ёу
ЁрAB
2=OA
2+OB
2ЃЌ
ЁрЃЈ1+mЃЉ
2+ЃЈ-
+
m
2ЃЉ
2=
+m
2+
m
4ЃЌ
НтЕУЃКm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
ЃЈ3ЃЉНтЗЈвЛЃКЩшAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ
-n2ЃЉЃЈnЃО0ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЌдђ
ЃЌ
ЃЈ1ЃЉЁСn+ЃЈ2ЃЉЁСmЕУЃЌ
(m+n)b=-(m2n+mn2)=-mn(m+n)ЃЌ
Ёр
b=-mnЃЈ8ЗжЃЉ
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
=ЃЌ
Ёр
=ЃЌ
Ёрmn=4ЃЌ
Ёр
b=-ЁС4=-2ЃЎ
гЩДЫПЩжЊВЛТлkЮЊКЮжЕЃЌжБЯпABКуЙ§ЕуЃЈ0ЃЌ-2ЃЉЃЎ
ЃЈЫЕУїЃКаДГіЖЈЕуCЕФзјБъОЭИј2ЗжЃЉ
НтЗЈЖўЃКЁпЕуAЪЧХзЮяЯпy=-
x
2ЩЯЕФЕуЃЌ
ЁрЩшAЃЈ-mЃЌ
-m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ
-n2ЃЉЃЈnЃО0ЃЉЃЌ
жБЯпABгыyжсЕФНЛЕуЮЊCЃЌИљОнS
ЁїAOB=S
ЬнаЮABFE-S
ЁїAOE-S
ЁїB0F=S
ЁїAOC+S
ЁїBOCЃЌ
ПЩЕУ
•(n2+m2)(m+n)-•m•m2-•n•n2=•OC•m+•OC•nЃЌ
ЛЏМђЃЌЕУ
OC=mnЃЎ
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
=ЃЌ
Ёр
=ЃЌ
Ёрmn=4ЃЌ
ЁрOC=2ЮЊЙЬЖЈжЕЃЎЙЪжБЯпABКуЙ§ЦфгыyжсЕФНЛЕуCЃЈ0ЃЌ-2ЃЉЃЌ
ЫЕУїЃКmnЕФжЕвВПЩвдЭЈЙ§вдЯТЗНЗЈЧѓЕУЃЎ
гЩЧАПЩжЊЃЌ
OA2=m2+m4ЃЌ
OB2=n2+n4ЃЌ
AB2=(m+n)2+(-m2+n2)2ЃЌ
гЩOA
2+OB
2=AB
2ЃЌЕУЃК
(m2+m4)+(n2+n4)=(m+n)2+(-m2+n2)2ЃЌ
ЛЏМђЃЌЕУmn=4ЃЎ
БОД№АИНіЙЉВЮПМЃЌШєгаЦфЫћНтЗЈЃЌЧыВЮееБОЦРЗжБъзМЦРЗжЃЎ

 НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ
НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ

 ПьРж5Мг2Н№ОэЯЕСаД№АИ
ПьРж5Мг2Н№ОэЯЕСаД№АИ
![]() ЕФаджЪЪБЃЌНЋвЛАбжБНЧШ§НЧАхЕФжБНЧЖЅЕужУгкЦНУцжБНЧзјБъЯЕЕФдЕу
ЕФаджЪЪБЃЌНЋвЛАбжБНЧШ§НЧАхЕФжБНЧЖЅЕужУгкЦНУцжБНЧзјБъЯЕЕФдЕу![]() ЃЌСНжБНЧБпгыИУХзЮяЯпНЛгк
ЃЌСНжБНЧБпгыИУХзЮяЯпНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧыНтД№вдЯТЮЪЬтЃК
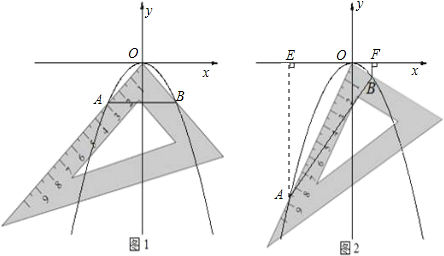
СНЕуЃЌЧыНтД№вдЯТЮЪЬтЃК![]() ЃЈШчЭМ1ЃЉЃЌЧѓ
ЃЈШчЭМ1ЃЉЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ![]() а§зЊЕНШчЭМ2ЫљЪОЮЛжУЪБЃЌЙ§
а§зЊЕНШчЭМ2ЫљЪОЮЛжУЪБЃЌЙ§![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌВтЕУ
ЃЌВтЕУ![]() ЃЌаДГіДЫЪБЕу
ЃЌаДГіДЫЪБЕу![]() ЕФзјБъЃЌВЂЧѓЕу
ЕФзјБъЃЌВЂЧѓЕу![]() ЕФКсзјБъЃЛ
ЕФКсзјБъЃЛ![]() а§зЊШЮвтНЧЖШЪБОЊЦцЕиЗЂЯжЃЌНЛЕу
а§зЊШЮвтНЧЖШЪБОЊЦцЕиЗЂЯжЃЌНЛЕу![]() ЁЂ
ЁЂ![]() ЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЌЪдЫЕУїРэгЩВЂЧѓГіИУЕуЕФзјБъЃЎ
ЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЌЪдЫЕУїРэгЩВЂЧѓГіИУЕуЕФзјБъЃЎ
 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ