
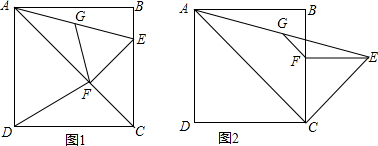
分析 (1)先根据勾股定理求出AE,再利用直角三角形斜边的中线等于斜边的一半,即可;
(2)先判断出DF=BF,然后判断出点A,F,E,B四点共圆,圆心为G,再判断出△BGF为等腰直角三角形,即可;
(3)先判断出△AGB≌△CGB,得到∠GBF=45°,再判断出△EFG≌△CFG,得到∠GFB=45°从而得到△BGF为等腰直角三角形,即可.
解答 解:(1)∵四边形ABCD为正方形,
∴∠ABC=90°,
根据勾股定理得,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10,
∵EF⊥AC,
∴∠AFE=90°,
∵点G是AE中点,
∴FG=$\frac{1}{2}$AE=5;
(2)连接BF,BG,如图1,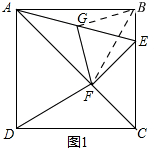
∵AC是正方形ABCD的对角线,
∴AB=AD,∠DAC=∠BAC,
∵AF=AF,
∴△AFD≌△AFB,
∴DF=BF,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠AEF=90°,
∴∠ABC=∠AEF=90°,
∴点A,F,E,B四点共圆,
∵点G是AE中点,
∴点G为点A,F,E,B四点共圆的圆心,
∵∠BAC=45°,
∴∠BGF=2∠BAC=90°,
在Rt△ABE中,BG=$\frac{1}{2}$AE,
在Rt△AFE中,FG=$\frac{1}{2}$AE,
∴BG=FG,
∴∠BGF=90°,
∴△BGF为等腰直角三角形,
∴BF=$\sqrt{2}$FG,
∵DF=BF,
∴DF=$\sqrt{2}$FG,
(3)BF=$\sqrt{2}$FG;连接BG,CG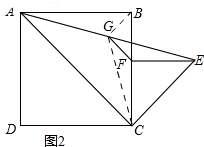
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
由旋转有,∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∴△AGB≌△CGB,
∴∠ABG=∠CBG=$\frac{1}{2}$∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG,
∴∠EFG=∠CFG=360°-∠BFE=360°-90°=270°,
∴∠EFG=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=$\sqrt{2}$FG.
点评 此题是四边形综合题,主要考查了正方形的性质,直角三角形的性质,全等三角形的判断方法和性质,勾股定理,旋转的特征,判断△BGF为等腰直角三角形是解本题的关键,作出辅助线是解本题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
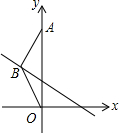 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{6}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com