
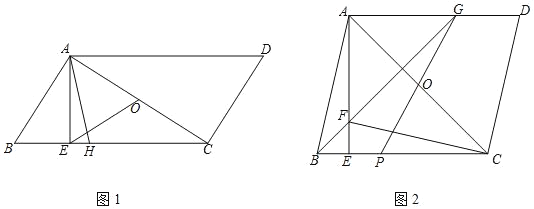
【题目】在平行四边形ABCD中,AE⊥BC于点E,AC为对角线,点O为对角线AC的中点.
(1)如图1,若AB⊥AC,AH平分∠BAC交BC于点H,连接EO,OE=2,CD=3,求AH的长;
(2)如图2,若AE=EC,过C作CD的垂线交AE于点F,连接BF并延长交AD于点G,连接GO并延长GO交BC于点P,求证:DG=2EP.
【答案】(1)AH=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
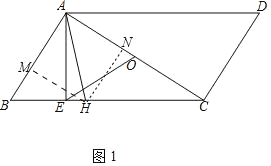
(1)如图1中,作HM⊥AB于M,HN⊥AC于N.利用面积法求出HN,再证明△AHN是等腰直角三角形即可解决问题.
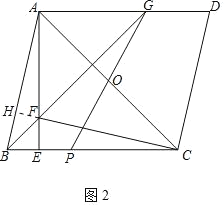
(2)如图2中,延长CF交AB于H.证明△AEB≌△CEF(ASA),推出BE=EF,证明△AOG≌△COP(ASA),推出AG=PC,再证明AG=AF=PC 推出EF=PE=BE即可解决问题.
(1)解:如图1中,作HM⊥AB于M,HN⊥AC于N.
∵AB⊥AC,
∴∠BAC=90°,
∵四边形ABCD是平行四边形,
∴AB=CD=3,
∵AE⊥BC,
∴∠AEC=90°,
∵OA=OC,OE=2,
∴AC=2OE=4,
∵AH平分∠BAC, HM⊥AB,HN⊥AC,
∴HM=HN.
∵S△ABC=![]() ABAC=
ABAC=![]() ABHM+
ABHM+![]() ACHN,
ACHN,
∴HM=HN=![]() ,
,
∵∠HAN=45°,∠ANH=90°,
∴AH=![]() HN=
HN=![]() .
.
(2)证明:如图2中,延长CF交AB于H.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵CF⊥CD,
∴CH⊥AB,
∴∠AHF=∠CEF=90°,∵∠AFH=∠CFE,
∴∠BAE=∠ECF,
∵∠AEB=∠CEF,AE=EC,
∴△AEB≌△CEF(ASA),
∴BE=EF,
∵AG∥PC,
∴∠OAG=∠OCP.
∵OA=OC,∠AOG=∠COP,
∴△AOG≌△COP(ASA),
∴AG=PC,
∵AD=BC,
∴DG=PB,
∵BE=EF,∠BEF=90°,
∴∠BEF=∠EFB=∠AFG=∠AGF=45°,
∴AG=AF,
∴AF=PC,
∵AE=EC,
∴EF=PE=BE,
∴DG=2PE.


科目:初中数学 来源: 题型:
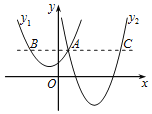
【题目】如图,抛物线y1:y=a1(x+1)2+1与y2:y=a2(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论,正确的是( )
A.![]() >
>![]() B.当
B.当![]() =
=![]() 时,x=1
时,x=1
C.当![]() >
>![]() 时,0≤x<1D.3AB=2AC
时,0≤x<1D.3AB=2AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
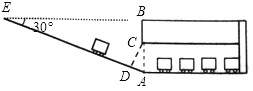
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.
(1)试求该校地下停车场的高度AC;
(2)求CD的高度,一辆高为6米的车能否通过该地下停车场(![]() =1.73,结果精确到0.1米).
=1.73,结果精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司推出一款新的电子产品,该产品有三种型号.通过市场调研后,按三种型号受消费者喜爱的程度分别对A型、B型、C型产品在成本的基础上分别加价20%,30%,45%出售(三种型号的成本相同).经过一个季度的经营后,发现C型产品的销量占总销量的![]() ,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.

(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com