
分析 (1)根据零指数幂的意义以及负整数指数幂的意义即可求出答案.
(2)根据分式的运算法则即可求出答案.
解答 解:(1)原式=9+1-1+(2$\sqrt{3}$-3$\sqrt{3}$)×$\frac{\sqrt{3}}{3}$
=9-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$
=9-3
=6,
(2)当a=3-2$\sqrt{2}$,b=3$\sqrt{2}$-3时,
原式=$\frac{1}{2a}$-$\frac{1}{a-b}$[$\frac{a-b}{2a}$-(a2-b2)]
=$\frac{1}{2a}$-$\frac{1}{a-b}$[$\frac{a-b}{2a}$-(a-b)(a+b)]
=$\frac{1}{2a}$-$\frac{1}{2a}$+a+b
=a+b
=3-2$\sqrt{2}$+3$\sqrt{2}$-3
=$\sqrt{2}$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


科目:初中数学 来源: 题型:选择题
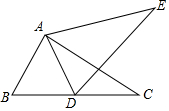 如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )
如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
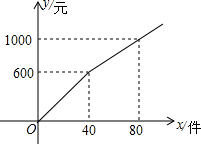 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 15元 | C. | 12.5元 | D. | 10元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
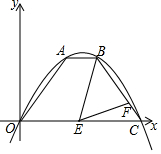 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com