
【题目】随着科技的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题.
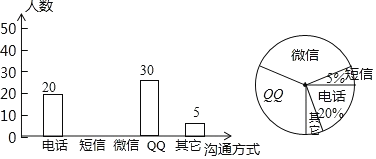
(1)这次统计共抽查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校共有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
【答案】(1)100,108°;(2)补图见解析;(3) 1000人; (4)树状图见解析,甲、乙两名同学恰好选中同一种沟通方式的概率为:![]() .
.
【解析】分析:(1)用电话的有20人占抽查人数的20%求抽查的人数;用QQ的人数占抽查总人数的比乘以360°;(2)用抽查的人数乘以5%即为用短信的人数,由此求出用微信的人数,即可补充条形图;(3)用抽查学生中用微信人数占抽查人数的比乘以全校学生数可求;(4)列树状图求出总的情况和符合条件的情况.
详解:(1)这次统计共抽查了20÷20%=100名;
在扇形统计图中,表示“QQ”的扇形圆心角的度数为![]() ×360=108°.
×360=108°.
故答案为100108°.
(2)喜欢用短信的人数为:100×5%=5名,喜欢用微信的人数为:100-20-5-30-5=40名.
补充图形如下:
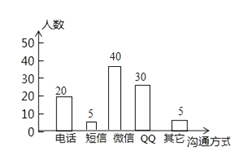
(3)因为该校共有2500名学生,所以估计该校最喜欢用“微信”进行沟通的学生有![]() ×2500=1000名.
×2500=1000名.
(4)列出树状图,如图所示
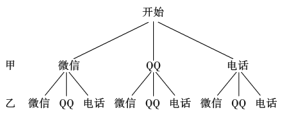
共有9种情况,其中两人恰好选中同一种沟通方式共有3种情况,
所以甲,乙两名同学恰好选中同一种沟通方式的概率为:![]() ,
,


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌ODFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
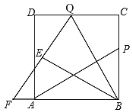
【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
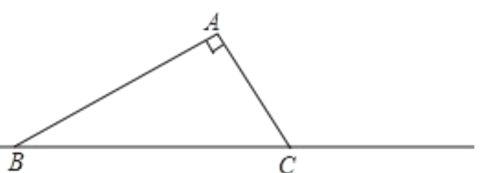
(2)直接写出A′B的长,A′B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com