
问题探究
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB= ,CD=
,CD= ,且
,且 ,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.

解:(1)如图①所示:
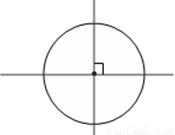
图①
(2)如图②,连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分。
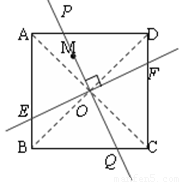
图②
理由如下:
∵点O是正方形ABCD对角线的交点,∴点O是正方形ABCD的对称中心。
∴AP=CQ,EB=DF。
在△AOP和△EOB中,
∵∠AOP=90°-∠AOE,∠BOE=90°-∠AOE,∴∠AOP=∠BOE。
∵OA=OB,∠OAP=∠EBO=45°,∴△AOP≌△EOB(ASA)。∴AP=BE=DF=CQ 。∴AE=BQ=CF=PD。
设点O到正方形ABCD一边的距离为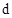 。
。
∴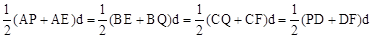
∴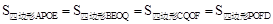 。
。
∴直线EF、PQ将正方形ABCD面积四等分。
(3)存在。当BQ=CD=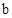 时,PQ将四边形ABCD面积二等分。
时,PQ将四边形ABCD面积二等分。
理由如下:
如图③,延长BA至点E,使AE=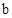 ,延长CD至点F,使DF=
,延长CD至点F,使DF=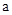 ,连接EF。
,连接EF。
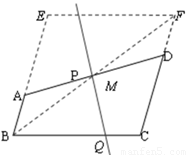
图③
∴BE∥CF,BE=CF。 ∴四边形BCFE为平行四边形。
∵BC=BE=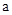 +
+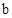 ,∴平行四边形DBFE为菱形。
,∴平行四边形DBFE为菱形。
连接BF交AD于点M,则△MAB≌△MDF。
∴AM=DM,即点P、M重合。
∴点P是菱形EBCF对角线的交点。
在BC上截取BQ=CD=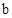 ,则CQ=AB=
,则CQ=AB=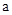 。
。
设点P到菱形EBCF一边的距离为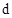 ,
,
∴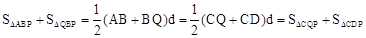 。
。
∴当BQ=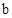 时,直线PQ将四边形ABCD的面积分成相等的两部分。
时,直线PQ将四边形ABCD的面积分成相等的两部分。
【解析】(1)圆内两条互相垂直的直径即达到目的。
(2)连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分。可应用△AOP≌△EOB得出结论。
(3)把原图补充成菱形,应用菱形的性质求解。


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
(本题满分12分)
问题探究
(1)请在图①的正方形![]() 内,画出使
内,画出使![]() 的一个点
的一个点![]() ,并说明理由.
,并说明理由.
(2)请在图②的正方形![]() 内(含边),画出使
内(含边),画出使![]() 的所有的点
的所有的点![]() ,并说明理由.
,并说明理由.
问题解决
(3)如图③,现在一块矩形钢板![]() .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的![]() 和
和![]() 钢板,且
钢板,且![]() .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点![]() 和
和![]() ,并求出
,并求出![]() 的面积(结果保留根号).
的面积(结果保留根号).
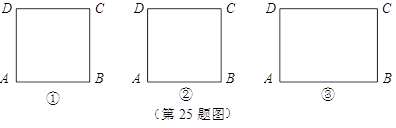
查看答案和解析>>
科目:初中数学 来源: 题型:
 内,画出使
内,画出使 的一个点
的一个点 ,并说明理由.
,并说明理由. 内(含边),画出使
内(含边),画出使 的所有的点
的所有的点 ,并说明理由.
,并说明理由. .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的 和
和 钢板,且
钢板,且 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点 和
和 ,并求出
,并求出 的面积(结果保留根号).
的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏镇江) 题型:解答题
(本题满分12分)
问题探究
(1)请在图①的正方形 内,画出使
内,画出使 的一个点
的一个点 ,并说明理由.
,并说明理由.
(2)请在图②的正方形 内(含边),画出使
内(含边),画出使 的所有的点
的所有的点 ,并说明理由.
,并说明理由.
问题解决
(3)如图③,现在一块矩形钢板 .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的 和
和 钢板,且
钢板,且 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点 和
和 ,并求出
,并求出 的面积(结果保留根号).
的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏镇江) 题型:解答题
(本题满分12分)
问题探究
(1)请在图①的正方形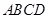 内,画出使
内,画出使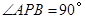 的一个点
的一个点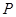 ,并说明理由.
,并说明理由.
(2)请在图②的正方形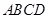 内(含边),画出使
内(含边),画出使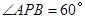 的所有的点
的所有的点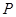 ,并说明理由.
,并说明理由.
问题解决
(3)如图③,现在一块矩形钢板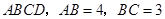 .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的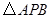 和
和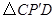 钢板,且
钢板,且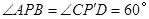 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点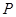 和
和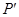 ,并求出
,并求出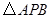 的面积(结果保留根号).
的面积(结果保留根号).
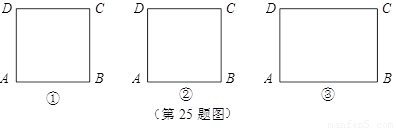
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com