【题目】已知四边形
中，
，则添加下列条件，不能使四边形成为平行四边形的是( )
A. 
B. 
C. 
D. 
【答案】D
【解析】
已知AB∥CD，可根据有一组边平行且相等的四边形是平行四边形来判定，也可根据两组分别平行的四边形是平行四边形来判定．
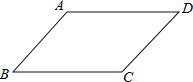
解：∵在四边形ABCD中，AB∥CD，
∴可添加的条件是：AB=CD，
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形），故选项A不符合题意；
∵AB∥CD，
∴∠B+∠C=180°，
∵∠B=∠D，
∴∠D+∠C=180°，
∴AD∥BC，
∴四边形ABCD是平行四边形，故选项D不符合题意；
∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，故选项C不符合题意；
∵AB∥CD，AD=BC无法得出四边形ABCD是平行四边形，故选项B符合题意．
故选：D．
阅读快车系列答案科目：初中数学 来源： 题型：
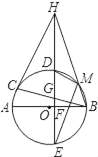
【题目】如图，AB，BC分别是⊙O的直径和弦，点D为
上一点，弦DE交⊙O于点E，交AB于点F，交BC于点G，过点C的切线交ED的延长线于H，且HC=HG，连接BH，交⊙O于点M，连接MD，ME．
求证：
（1）DE⊥AB；
（2）∠HMD=∠MHE+∠MEH．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 为满足社区居民健身的需要，市政府准备采购若干套健身器材免费提供给社区，经考察，劲松公司有
两种型号的健身器可供选择.
（1）劲松公司2015年每套
型健身器的售价为
万元，经过连续两年降价，2017年每套售价为
万元，求每套型健身器年平均下降率
；
（2）2017年市政府经过招标，决定年内采购并安装劲松公司两种型号的健身器材共
套，采购专项费总计不超过
万元，采购合同规定：每套型健身器售价为
万元，每套
型健身器售价我
万元.
①型健身器最多可购买多少套？
②安装完成后，若每套型和型健身器一年的养护费分别是购买价的
和
.市政府计划支出
万元进行养护.问该计划支出能否满足一年的养护需要？
查看答案和解析>>
科目：初中数学 来源： 题型：
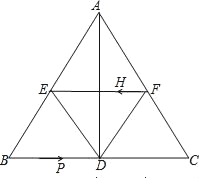
【题目】如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm，E点F点分别为AB，AC的中点．
（1）求证：四边形AEDF是菱形；
（2）求菱形AEDF的面积；
（3）若H从F点出发，在线段FE上以每秒2cm的速度向E点运动，点P从B点出发，在线段BC上以每秒3cm的速度向C点运动，问当t为何值时，四边形BPHE是平行四边形？当t取何值时，四边形PCFH是平行四边形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法错误的有（ ）个
①互为相反数的数的立方根也互为相反数；
②
不是整式；
③算术平方根等于它本身的数只有零；
④实数和数轴上的点一一对应；
⑤任何两数相加，和不小于任何一个加数．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
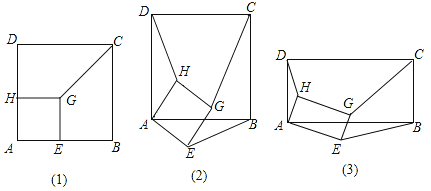
【题目】（1）(3分)如图（1），正方形AEGH的顶点E、H在正方形ABCD的边上，直接写出HD∶GC∶EB的结果（不必写计算过程）；
（2）(3分)将图（1）中的正方形AEGH绕点A旋转一定角度，如图（2），求HD∶GC∶EB；
（3）(2分)把图（2）中的正方形都换成矩形，如图（3），且已知ＤA∶AB＝HA∶AE＝m: n，此时HD∶GC∶EB的值与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，在
中，
，过点
的直线
，
为
边上一点，过点作
，交直线
于点
，垂足为点
，连接
.
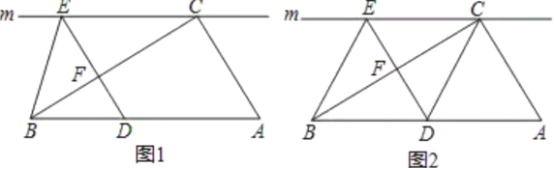
（1）求证：
；
（2）如图
，当点是中点时，连接
.
①四边形
是什么特殊四边形？说明你的理由；
②当
时，四边形是正方形.（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中,正确的是( )
A.单项式 
的系数是-2，次数是3B.单项式a的系数是0，次数是0
C.
是三次三项式，常数项是1D.单项式
的次数是2，系数为
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB与CD相交于O．OF是∠BOD的平分线，OE⊥OF．
（1）若∠BOE比∠DOF大38°，求∠DOF和∠AOC的度数；
（2）试问∠COE与∠BOE之间有怎样的大小关系？请说明理由．
（3）∠BOE的余角是 ，∠BOE的补角是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com