
 如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是
如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是

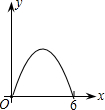

 AB,然后表示出DG,再利用勾股定理列式表示出PD2,代入等式得到y、x的函数关系式,从而得解.
AB,然后表示出DG,再利用勾股定理列式表示出PD2,代入等式得到y、x的函数关系式,从而得解. 解:如图,延长PF交AB于点G,
解:如图,延长PF交AB于点G, AB=
AB= ×6=3,
×6=3,

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
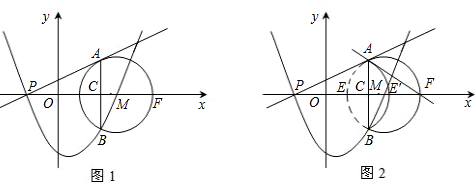
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在平面直角坐标系中,已知点M的坐标是(3,0),半径为2的⊙M交x轴于E、F
两点,过点P(-1,0)作⊙M的切线,切点为点A,过点A作AB⊥x轴于点C,交⊙M于
点B。抛物线y=ax2+bx+c经过P、B、M三点。
1.(1)求该抛物线的函数表达式;(3分)
2.(2)若点Q是抛物线上一动点,且位于P、B两点之间,设四边形APQB的面积为S,点Q的
横坐标为x,求S与x之间的函数关系式,并求S的最大值和此时点Q的坐标;(4分)
3.(3)如图2,将弧AEB沿弦AB对折后得到弧AE′B,试判断直线AF与弧AE′B的位置关系,
并说明理由。(3分)
查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考模拟数学卷 题型:解答题
如图1,在平面直角坐标系中,已知点M的坐标是(3,0),半径为2的⊙M交x轴于E、F
两点,过点P(-1,0)作⊙M的切线,切点为点A,过点A作AB⊥x轴于点C,交⊙M于
点B。抛物线y=ax2+bx+c经过P、B、M三点。
【小题1】(1)求该抛物线的函数表达式;(3分)
【小题2】(2)若点Q是抛物线上一动点,且位于P、B两点之间,设四边形APQB的面积为S,点Q的
横坐标为x,求S与x之间的函数关系式,并求S的最大值和此时点Q的坐标;(4分)
【小题3】(3)如图2,将弧AEB沿弦AB对折后得到弧AE′B,试判断直线AF与弧AE′B的位置关系,
并说明理由。(3分)
查看答案和解析>>
科目:初中数学 来源:2013年广东省中考数学模拟试卷(六)(解析版) 题型:解答题
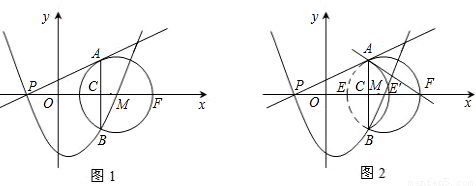
查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市宝安区中考模拟数学卷 题型:解答题
如图1,在平面直角坐标系中,已知点M的坐标是(3,0),半径为2的⊙M交x轴于E、F
两点,过点P(-1,0)作⊙M的切线,切点为点A,过点A作AB⊥x轴于点C,交⊙M于
点B。抛物线y=ax2+bx+c经过P、B、M三点。

1.(1)求该抛物线的函数表达式;(3分)
2.(2)若点Q是抛物线上一动点,且位于P、B两点之间,设四边形APQB的面积为S,点Q的
横坐标为x,求S与x之间的函数关系式,并求S的最大值和此时点Q的坐标;(4分)
3.(3)如图2,将弧AEB沿弦AB对折后得到弧AE′B,试判断直线AF与弧AE′B的位置关系,
并说明理由。(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com