
分析 (1)根据分式的加法和除法可以解答本题;
(2)根据分式加法可以解答本题;
(3)先化简题目中的式子,然后将a、b的值代入化简后的式子即可解答本题.
解答 解:(1)($\frac{1}{x-y}$+$\frac{1}{x+y}$)÷$\frac{xy}{{x}^{2}-{y}^{2}}$
=$\frac{x+y+x-y}{(x-y)(x+y)}×\frac{(x+y)(x-y)}{xy}$
=$\frac{2x}{xy}$
=$\frac{2}{y}$;
(2)$\frac{2m-n}{n-m}$+$\frac{m}{m-n}$+$\frac{n}{n-m}$
=$\frac{2m-n-m+n}{n-m}$
=$\frac{m}{n-m}$;
(3)($\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$)÷($\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$)+1
=$\frac{a(a-b)-{a}^{2}}{(a-b)^{2}}÷\frac{a(a-b)-{a}^{2}}{(a+b)(a-b)}+1$
=$\frac{-ab}{(a-b)^{2}}×\frac{(a+b)(a-b)}{-ab}+1$
=$\frac{a+b}{a-b}+1$
=$\frac{a+b+a-b}{a-b}$
=$\frac{2a}{a-b}$,
当a=$\frac{2}{3}$,b=-3时,原式=$\frac{2×\frac{2}{3}}{\frac{2}{3}-(-3)}=\frac{4}{11}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB,
小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校教导处为了了解本校初二学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的初二学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示).请结合统计图中提供的信息,回答下列问题:
某校教导处为了了解本校初二学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的初二学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示).请结合统计图中提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D,E分别是AB,AC的中点,CD=2DE,延长ED到点F,使得DF=CD,连接BF.
如图,在△ABC中,D,E分别是AB,AC的中点,CD=2DE,延长ED到点F,使得DF=CD,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
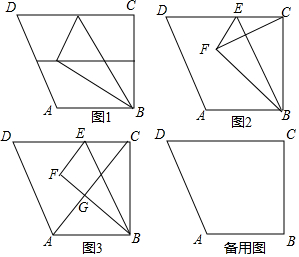
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com