
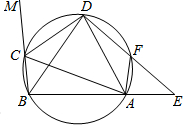
 如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.
如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.分析 (1)由圆内接四边形的性质及圆的性质可求得∠DBA=∠DAB,从而可证明AD=BD;
(2)由条件可证得△AEF∽△DAC,再利用相似三角形的性质可求得DE的长.
解答 (1)证明:
∵CD平分∠ACM,
∴∠ACD=∠MCD,
∵四边形ABCD为圆内接四边形,
∴∠MCD=∠BAD,
又∠ACD=∠ABD,
∴∠BAD=∠ABD,
∴AD=BD;
(2)解:
∵BD=AD,BC=AF,
∴$\widehat{BD}$=$\widehat{AD}$,$\widehat{BC}$=$\widehat{AF}$,
∴$\widehat{CD}$=$\widehat{DF}$,
∴CD=DF,
∵BC=AF,
∴∠BDC=∠ADF,
∴∠CDA=∠BDF=∠EAF,
由(1)可知∠DCA=∠DBA,且∠EFA=∠DBA,
∴∠DCA=∠EFA,
∴△AEF∽△DAC,
∴$\frac{EF}{AC}$=$\frac{AF}{CD}$,
∴$\frac{EF}{AC}$=$\frac{AF}{DF}$,$\frac{EF}{10}$=$\frac{3}{DF}$,
∴EF•DF=30,
∵DF:FE=3:2,
∴设DF=3x,则FE=2x,
∴6x2=30,解得x=$\sqrt{5}$,
∴DE=DF+FE=5x=5$\sqrt{5}$.
点评 本题主要考查圆的有关性质及相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,特别是在(2)中找出三角形相似的条件是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知三角形ABC
如图,已知三角形ABC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,BC=10$\sqrt{3}$,试求CD的长.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,BC=10$\sqrt{3}$,试求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某镇枇杷园的枇杷除了运往市区销售外,还可以让市民亲自去园内采摘购买,已知今年3月份该枇杷在市区、园区的销售价格分别为6元/千克、4元/千克,今年3月份一共销售了3000千克,总销售额为16000元.
某镇枇杷园的枇杷除了运往市区销售外,还可以让市民亲自去园内采摘购买,已知今年3月份该枇杷在市区、园区的销售价格分别为6元/千克、4元/千克,今年3月份一共销售了3000千克,总销售额为16000元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一天之中,海水的水深是不同的,如图是某港口从0时到12时的水深情况,结合图象回答下列问题:
一天之中,海水的水深是不同的,如图是某港口从0时到12时的水深情况,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com