
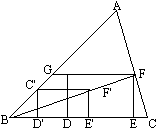
已知:锐角△ABC如图所示
求作:内接矩形DEFG,使DE在BC边上,点G,F分别在AB,AC边上,且DE∶GD=2∶1
|
解:作法: (1)作矩形 (2)连结 (3)过F作FE⊥BC于E,作FG∥BC交AB于G; (4)过G作GD⊥BC于D; 则四边形DEFG就是所求的矩形. 证明:由作法知:∠FED=∠GDE= 由作法知: 分析:求作的矩形要满足四个条件:①DE在BC边上;②G在AB边上;③F在AC边上;④DE∶DG=2∶1.要同时满足这么多条件比较困难,不妨先放弃一个条件,比如放弃“F在AC边上”这个条件,那样的矩形就比较好作.如图中的 点拨:像这样的作图题,由已知条件不仅规定了图形的形状、大小,而且限制了图形了位置,必须内接于一个三角形,这叫做定位作图,而相反,一般的作图题,只要求形状大小,而不限制位置,就叫做活位作图.也就是说定定位作图的要求较高,要更灵活地运用相似的有关知识.思考:如果在题中,先放弃“DE在BC上”这个条件作相似的图形,那么位似中心应取在哪里?试一试. |


科目:初中数学 来源:数学教研室 题型:044
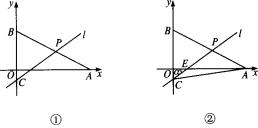
(1)如图①,当PB=PC时,求点P的坐标;
(2)如图②,设直线l与x轴所夹的锐角为a,且tana=![]() ,连结AC,求直线ι与x轴的交点E的坐标及△PAC的面积.
,连结AC,求直线ι与x轴的交点E的坐标及△PAC的面积.
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:022
(2)(浙江杭州2003年中考试题)如图,锐角三角形ABC的边AB、AC上的高线CE和 BF相交于点D.请写出图中的两对相似三角形________(用相似符号连接).

(3)(广西桂林2003年中考试题)如图,在直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C为顶点组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).

查看答案和解析>>
科目:初中数学 来源: 题型:047
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
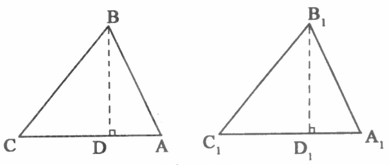
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,-
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com