
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬��x����D��C���㣬����
����A��B���㣬��x����D��C���㣬����![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��
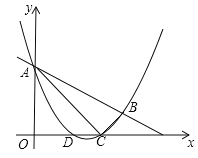
��1���������ߵĽ���ʽ��
��2��PΪy���Ҳ���������һ���㣬����![]() ������P��
������P��![]() ��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ������������
��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ������������![]() ���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����EΪ�߶�![]() ��һ�㣨�����˵㣩������
��һ�㣨�����˵㣩������![]() ��һ����M�ӵ�D���������߶�
��һ����M�ӵ�D���������߶�![]() ��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�
��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�
����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�
���𰸡���1��![]() ����2�����ڣ�����P������Ϊ��11��36����
����2�����ڣ�����P������Ϊ��11��36����![]() ��
��![]() ����
����![]() ��
��![]() ������3������E������Ϊ��2��1��ʱ����M�������˶�����ʱ������
������3������E������Ϊ��2��1��ʱ����M�������˶�����ʱ������
��������
��1����A��C������������߽���ʽ�����ɵõ�����m��n�ķ����飬�ⷽ���鼴�����m��n��ֵ�������ɵý����
��2�������ֱ��AB�������ߵĽ���B�����꣬�����ù��ɶ����涨���жϳ���ABC��ֱ�������Σ��Ӷ���ACB��90�㣻����P��PG��y����G�����P�ĺ�����Ϊx���ٷֵ�G�ڵ�A���·��͵�G�ڵ�A���Ϸ����ֱ��������������ε������ú�x�Ĵ���ʽ��ʾ����P�����꣬Ȼ����������ߵĽ���ʽ�������x��ֵ�����⼴�ý����
��3����ͼ3����A������AF��x�ᣬ��D������DF��y�ᣬDF��AC���ڵ�E��DF��AF���ڵ�F������õ�M�������˶��е���ʱΪ��t��![]() ��DE+EF=DF����ʱ��M�������˶��е���ʱ���٣�Ȼ�������D�����D�ĺ��������ֱ��AC����ʽ����������.
��DE+EF=DF����ʱ��M�������˶��е���ʱ���٣�Ȼ�������D�����D�ĺ��������ֱ��AC����ʽ����������.
�⣺��1����![]() ��
��![]() ���������ߵĽ���ʽ���ã�
���������ߵĽ���ʽ���ã�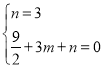 ����ã�
����ã� ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2�����ڵ�P��ʹ����A��P��QΪ��������������ACB���ƣ�
���� ����ã�
����ã�![]() ��
��![]() �����B��������4��1����
�����B��������4��1����
��C��3��0����B��4��1����A��0��3����
��AB2��20��BC2��2��AC2��18��
��BC2+AC2��AB2�����ABC��ֱ�������Σ�
���ACB��90�㣬��tan��BAC��![]() ��
��
����P��PG��y����G�����PGA��90�㣮
���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG��x��
��PQ��PA����ACB��90�㣬���APQ����ACB��90�㣮
����G�ڵ�A���·���
����ͼ2�٣�����PAQ����CABʱ�����PAQ�ס�CAB��
�ߡ�PGA����ACB��90�㣬��PAQ����CAB��
���PGA�ס�BCA����![]() ��
��
��AG��3PG��3x����P��x��3��3x����
��P��x��3��3x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2����1����ȥ����
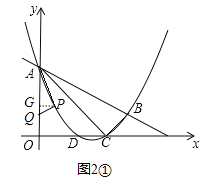
����ͼ2�ڣ�����PAQ����CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã�AG��![]() PG��
PG��![]() x����P��x��3��
x����P��x��3��![]() x����
x����
��P��x��3��![]() x������
x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��![]() ��
��
��P��![]() ��
��![]() ����
����

����G�ڵ�A���Ϸ���
�ٵ���PAQ����CABʱ�����PAQ�ס�CAB��
�ߡ�PGA�ס�BCA����![]() ��
��
��AG��3PG��3x����P��x��3+3x����
��P��x��3+3x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��11��
���P��������11��36����
�ڵ���PAQ����CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã�AG��![]() PG��
PG��![]() x����P��x��3+
x����P��x��3+![]() x����
x����
��P��x��3+![]() x������
x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��![]() ��
��
��P��![]() ��
��![]() ����
����
�������������������ĵ�P������Ϊ��11��36����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3����ͼ3����A������AF��x�ᣬ��D������DF��y�ᣬDF��AC���ڵ�E��DF��AF���ڵ�F��
��A��0��3����C��3��0������lAC��y����x+3��
��OA��OC����AOC��90�㣬���ACO��45�㣬
��AF��OC�����FAE��45�㣬
��EF��AEsin45�㣽![]() ��
��
���M�������˶��е���ʱΪ��t��![]() ��DE+EF=DF������AF��DFʱ��DE+EFȡ����СֵDF����ʱ��M�������˶��е���ʱ���٣�
��DE+EF=DF������AF��DFʱ��DE+EFȡ����СֵDF����ʱ��M�������˶��е���ʱ���٣�
�������ߵĽ���ʽΪ![]() ����y=0����
����y=0����![]() ����ã�
����ã�![]() ��
��
��D������Ϊ��2��0������E�������Ϊ2����x��2����lAC��y����x+3����y��1������E��2��1����
������E������Ϊ��2��1��ʱ����M�������˶�����ʱ���٣�



 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳���װ���������з��֣�ij��ͯװƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ��Ϊ��ӭ������һ����ͯ�ڣ��̳�������ȡ�ʵ��Ľ��۴�ʩ������������������ӯ�������ٿ�棬���г����鷢�֣����ÿ��ͯװÿ����4Ԫ����ôƽ��ÿ��Ϳɶ��۳�8����
��1�����̳�Ҫ��ƽ��ÿ������������ͯװ��ӯ��1200Ԫ����ôÿ��ͯװӦ���۶���Ԫ��
��2�����̳�Ҫ��ƽ��ÿ������������ͯװ��ӯ����࣬��ôÿ��ͯװӦ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ���ཻ�ڵ�A������
��ͼ���ཻ�ڵ�A������![]() �ύ�ڵ�C��S��AOC=15����D���߶�AC��һ�㣬CD��AC=2��3��
�ύ�ڵ�C��S��AOC=15����D���߶�AC��һ�㣬CD��AC=2��3��
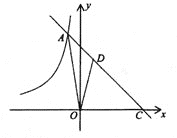
��1����![]() ��ֵ��
��ֵ��
��2�����D�����ꣻ
��3������ͼ��ֱ��д����![]() ʱ����ʽ
ʱ����ʽ![]() ��
��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ����ڵ�F.
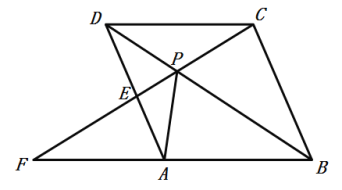
��1����֤��![]() .
.
��2�����![]() �����߶�PC�ij�.
�����߶�PC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+2kx+k2+k+3=0�������ֱ���x1��x2����x1��1��2+��x2��1��2����Сֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��y=kx+b ������A����![]() ��0���͵�B��2��5����
��0���͵�B��2��5����
��1����ֱ��l1��y��Ľ������ꣻ
��2������C��a��a+2�����D��ֱ��l1�ϣ�����D��ֱ��l2��x�������ύ�ڵ� E����AC=CD=CE ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
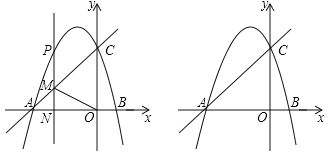
����Ŀ����ͼ��������y����![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ��C��ֱ��y��
x2+bx+c��x�ύ��A��B���㣬��y�ύ��C��ֱ��y��![]() x+3������A��C��
x+3������A��C��
��1���������ߵĽ���ʽ��
��2��P����������һ���㣬��P��PM��y�ύֱ��AC�ڵ�M�����P�ĺ�����Ϊt��
�����Ե�C��O��M��PΪ������ı�����ƽ���ı��Σ���t��ֵ��
�ڵ�����MP��AC��MO��һ������ƽ�������������ߵļн�ʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����λ��t��![]() ������a��b��c��ȫ����Ҷ���Ϊ0�����������и���λ�ϵ����ֱؿɵõ�һ���������һ����С���������������С���IJ����ԭ���IJ�������ΪT��t�������磬539�IJ���T��539����953��359��594��
������a��b��c��ȫ����Ҷ���Ϊ0�����������и���λ�ϵ����ֱؿɵõ�һ���������һ����С���������������С���IJ����ԭ���IJ�������ΪT��t�������磬539�IJ���T��539����953��359��594��
��1���������Ϸ������T��268������ ����T��513������ ����
��2����֪��λ��![]() ������a��b��1���IJ���T��
������a��b��1���IJ���T��![]() ����495���Ҹ���λ�ϵ�����֮��Ϊ3�ı����������з�����������λ����ֵ��
����495���Ҹ���λ�ϵ�����֮��Ϊ3�ı����������з�����������λ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��l1��l2��l3�����ཻ��A��B��C���㣬������y��������ֱ��ڵ�D��E��F����A��B��C���������ֱ�Ϊ��1��yA������2��yB������3��yC������OD��DE��1�������н�����ȷ�ĸ����ǣ���������EC��3EA����S��ABC��1����OF��5����2yA��yA��yC��2
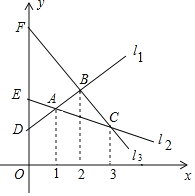
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com