
【题目】喜欢探究的亮亮同学拿出形状分别是长方形和正方形的两块纸片,其中长方形纸片的长为![]() ,宽为
,宽为![]() ,且两块纸片面积相等.
,且两块纸片面积相等.
(1)亮亮想知道正方形纸片的边长,请你帮他求出正方形纸片的边长;(结果保留根号)
(2)在长方形纸片上截出两个完整的正方形纸片,面积分别为![]() 和
和![]() ,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:
,亮亮认为两个正方形纸片的面积之和小于长方形纸片的总面积,所以一定能截出符合要求的正方形纸片来,你同意亮亮的见解吗?为什么?(参考数据:![]() ,
,![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
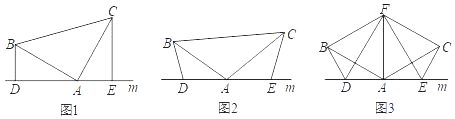
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从邵阳市到长沙的高铁列车里程比普快列车里程缩短了75千米,运行时间减少了4小时,已知邵阳市到长沙的普快列车里程为306千米,高铁列车平均时速是普快列车平均时速的3.5倍.
(1)求高铁列车的平均时速;
(2)某日刘老师从邵阳火车南站到长沙市新大新宾馆参加上午11:00召开的会议,如果他买到当日上午9:20从邵阳市火车站到长沙火车南站的高铁票,而且从长沙火车南站到新大新宾馆最多需要20分钟.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村老杨家有耕地和林地共24公顷,今年每公顷耕地纯收入为5500元,每公顷林地纯收入为6000元,耕地与林地的纯收入共137000元,为保护生态环境,增加收入,老杨计划将部分耕地改为林地(改后每公顷耕地,林地纯收入不变),要使改后的纯收入为140000元.问:
(1)老杨家原有耕地,林地各多少公顷?
(2)老杨应将多少公顷耕地改为林地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.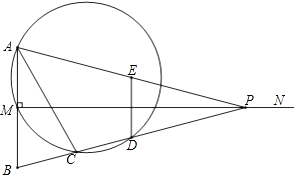
(1)当∠APB=28°时,求∠B和 ![]() 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B= ![]() ∠D,∠C=
∠D,∠C= ![]() ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;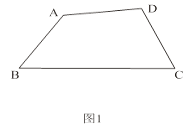
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.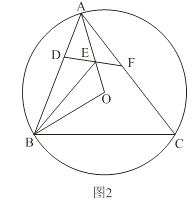
求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.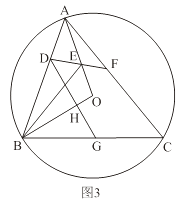
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
则符合这一结果的实验最有可能的是( )
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是梅花
B.抛一枚硬币,出现反面的概率
C.袋子里有除了颜色都一样3个红球,2个白球,随机摸一个球是白球的概率
D.抛一个质地均匀的正六面体骰子,向上的面点数大于4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com