
 如图,E是△ABC中BC边上的一点,且BE=$\frac{1}{3}$BC;点D是AC上一点,且AD=$\frac{1}{4}$AC,S△ABC=24,则S△BEF-S△ADF=( )
如图,E是△ABC中BC边上的一点,且BE=$\frac{1}{3}$BC;点D是AC上一点,且AD=$\frac{1}{4}$AC,S△ABC=24,则S△BEF-S△ADF=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 过D作DG∥AE交CE于G,根据已知条件得到CG=3EG,求得AE=$\frac{4}{3}$DG,CE=$\frac{4}{3}$CG,求出S△ABD=$\frac{1}{4}$S△ABC=6.由EC=2BE,S△ABC=24,得到S△ABE=$\frac{1}{3}$S△ABC=8,于是得到结论.
解答 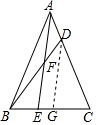 解:过D作DG∥AE交CE于G,
解:过D作DG∥AE交CE于G,
∵AD=$\frac{1}{4}$AC,
∴CG=3EG,
∴AE=$\frac{4}{3}$DG,CE=$\frac{4}{3}$CG,
∵EC=2BE,
∴BE=2EG,
∴EF=$\frac{2}{3}$DG,
∴AF=$\frac{2}{3}$DG,
∴EF=AF,
∵S△ABC=24,
∴S△ABD=$\frac{1}{4}$S△ABC=6.
∵EC=2BE,S△ABC=24,
∴S△ABE=$\frac{1}{3}$S△ABC=8,
∵S△ABE-S△ABD=(S△ABF+S△BEF)-(S△ADF+S△ABF)=S△BEF-S△ADF,
即S△BEF-S△ADF=S△ABE-S△ABD=8-6=2.
故选B.
点评 本题考查了三角形的中位线的性质,三角形的面积,关键知道当高相等时,面积等于底边的比,根据此可求出三角形的面积,然后求出差.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
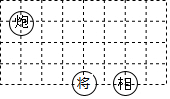 如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“相”位于(1,-2),则“炮”位于点( )
如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“相”位于(1,-2),则“炮”位于点( )| A. | (1,4) | B. | (4,1) | C. | (-4,1) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
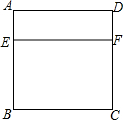 如图,点E和点F分别是正方形ABCD的边AB、DC上的两个动点,EF∥BC,点E从点A向点B匀速运动,设四边形EBCF的面积为s,两点运动的时间为t,则图中能较好反映s与t的函数关系的图象是( )
如图,点E和点F分别是正方形ABCD的边AB、DC上的两个动点,EF∥BC,点E从点A向点B匀速运动,设四边形EBCF的面积为s,两点运动的时间为t,则图中能较好反映s与t的函数关系的图象是( )| A. | 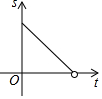 | B. | 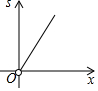 | C. | 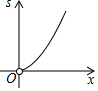 | D. | 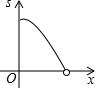 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | x>4,x≤1 | B. | x<4,x≥-1 | C. | x>4,x>-1 | D. | x≤4,x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
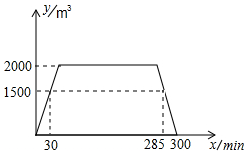 某游泳池一天要经过“注水-保持-排水”三个过程,如图,图中折线表示的是游泳池在一天某一时间段内池中水量y(m3)与时间x(min)之间的关系.
某游泳池一天要经过“注水-保持-排水”三个过程,如图,图中折线表示的是游泳池在一天某一时间段内池中水量y(m3)与时间x(min)之间的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com