

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先利用勾股定理计算出所有三角形的边长,然后根据三组对应边的比相等的两个三角形相似对四组图形矩形判断.
解答 解:AB=2,BC=$\sqrt{2}$,AC=$\sqrt{10}$,
对于图①,三角形三边为2,3$\sqrt{2}$,2$\sqrt{5}$,因为$\frac{\sqrt{2}}{2}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{10}}{2\sqrt{5}}$,所以图①的三角形与△ABC相似;
对于图②,三角形三边为2$\sqrt{5}$,2$\sqrt{10}$,10,因为$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{2\sqrt{10}}{2}$=$\frac{\sqrt{10}}{10}$,所以图②的三角形与△ABC相似;
对于图③,三角形三边为2$\sqrt{2}$,$\sqrt{10}$,5,因为$\frac{\sqrt{2}}{2\sqrt{2}}$≠$\frac{2}{\sqrt{10}}$=$\frac{\sqrt{10}}{5}$,所以图③的三角形不与△ABC相似;
对于图④,三角形三边为$\sqrt{10}$,2$\sqrt{5}$,5$\sqrt{2}$,因为$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{10}}{5\sqrt{2}}$,所以图④的三角形与△ABC相似.
故选C.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似.解决本题的关键是利用勾股定理分别计算出图中所有三角形的边长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
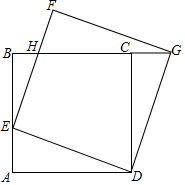 如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB-BC向终点C运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).设点E运动的速度为每秒1个单位,运动的时间为x 秒.
如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB-BC向终点C运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).设点E运动的速度为每秒1个单位,运动的时间为x 秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题




查看答案和解析>>
科目:初中数学 来源: 题型:解答题
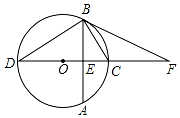 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x2 | B. | x1>x2 | C. | x1=x2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com