
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
分析 (1)生产A款家具x套,则生产B种家具(50-x)套,两种家具的获利的和就是总获利y,据此列出函数解析式;
(2)根据两种原料必须够用即可列不等式组求得x的范围,然后根据函数的性质求解.
解答 解:(1)生产A款家具x套,则生产B种家具(50-x)套,
则y=600x+400(50-x),即y=200x+20000;
(2)根据题意得:$\left\{\begin{array}{l}{3x+5(50-x)≤210}\\{7x+3(50-x)≤250}\end{array}\right.$,
解得:20≤x≤25.
则当x=25时,50-25=25(套),
则安排生产A和B款都是25套时,或得的利润最大.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
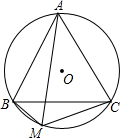 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
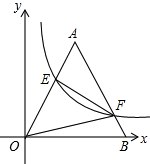 若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.
若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.| 每月用水量 (m3) | 单价(元/m3) |
| 不超出10m3的部分 | a |
| 超出10m3的部分 | a+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
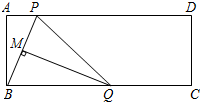 如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.
如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com