
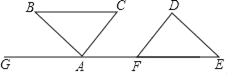
【题目】如图,点A、F在线段GE上,AB∥DE,BC∥GE,AC∥DF,AB=DE
(1)请说明:△ABC≌△DEF;
(2)连接BF、CF、CE,请你判断BF与CE之间的关系?并说明理由
【答案】(1)证明见解析;(2)结论:BF∥CE,BF=CE,理由见解析.
【解析】
(1)由平行线的性质可得∠ABC=∠DEF,∠BCA=∠DFE,进而可证△ABC和△DEF全等.(2)由(1)可知 △ABC≌△DEF;则BC=EF,又BC∥EF,则四边形BFEC是平行四边形,所以BF∥CE,BF=EC.
(1)证明:∵BC∥GE,
∴∠ABC=∠BAG,∠BCA=∠CAF,
∵AB∥DE,AC∥DF,
∴∠BAG=∠DEF,∠DFE=∠CAF,
∴∠ABC=∠DEF,∠BCA=∠DFE,
∵AB=DE,
∴△ABC≌△DEF.
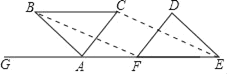
(2)结论:BF∥CE,BF=CE,理由如下,
∵△ABC≌△DEF,
∴BC=EF,
∵BC∥EF,
∴四边形BFEC是平行四边形,
∴BF∥CE,BF=EC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标
(3)求出△A1B1C1的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1,有下列四个结论:①abc<0,②a<﹣![]() ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是大家公认的![]() 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解![]() 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生![]() 手机的使用情况
手机的使用情况
D.该调査中的样本容量是500位大学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
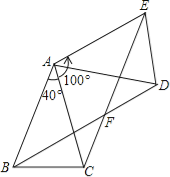
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整.
解:∵DE∥BC(已知)
∴______(两直线平行,内错角相等)
∵EF∥AB(已知)
∴∠ABC=∠EFC(______)
∴∠DEF=∠ABC=40°(等量代换)
应用:如图2,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线R上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ∥
∥![]() ,直线
,直线![]() 和
和![]() ,
,![]() 分别交于点
分别交于点![]() .A为
.A为![]() 上一点,B为
上一点,B为![]() 上一点,P为
上一点,P为![]() 上一动点。
上一动点。
(1)如果P在C、D之间运动,如图①(点P与点C、D不重合),请说明:![]()
(2)如果P在CD两点的外侧运动,如图②、图③(点P与点C、D不重合),问∠APB,![]() ,
,![]() 有何关系,请直接写出结论。
有何关系,请直接写出结论。



图① 图② 图③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com