
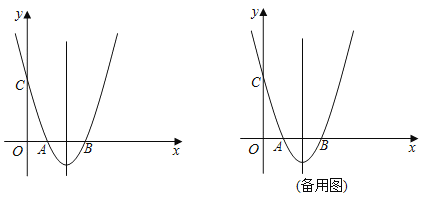
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
【答案】(1)y=x2﹣4x+3,抛物线顶点坐标是(2,﹣1);(2)P(![]() ,
,![]() );(3)抛物线平移的距离为
);(3)抛物线平移的距离为![]() .
.
【解析】
(1)由抛物线的对称性质得到点B的坐标,把点A、B的坐标分别代入抛物线解析式,列出方程组,通过解方程组求得系数的值;根据抛物线解析式求得顶点坐标;
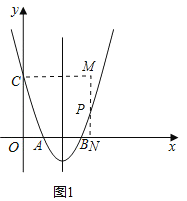
(2)过点P作PN⊥x轴于N,过点C作CM⊥PN,交NP的延长线于点M,构造矩形COMN和直角三角形,利用锐角三角函数的定义求得![]() ,故设PM=a,MC=3a,PN=3-a.易得P(3a,3-a),由二次函数图象上点的坐标特征列出关于a的方程,通过解方程求得a的值,易得点P的坐标;
,故设PM=a,MC=3a,PN=3-a.易得P(3a,3-a),由二次函数图象上点的坐标特征列出关于a的方程,通过解方程求得a的值,易得点P的坐标;
(3)设抛物线平移的距离为m,得y=(x-2)2-1-m.从而求得D(2,-1-m).过点D作直线EF∥x轴,交y轴于点E,交PQ延长线于点F.易推知∠EOD=∠QDF,则tan∠EOD=tan∠QDF,根据锐角三角函数定义列出关于m的方程,通过解方程求得m的值.
解:(1)∵对称轴为直线x=2,点A的坐标为(1,0),
∴点B的坐标是(3,0).
将A(1,0),B(3,0)分别代入y=x2+bx+c,得
![]() .
.
解得![]() .
.
则该抛物线解析式是:y=x2﹣4x+3.
由y=x2﹣4x+3=(x﹣2)2﹣1知,该抛物线顶点坐标是(2,﹣1);
(2)如图1,过点P作PN⊥x轴于N,过点C作CM⊥PN,交NP的延长线于点M,
∵∠CON=90°,
∴四边形CONM是矩形.
∴∠CMN=90°,CO=MN、
∴y=x2﹣4x+3,
∴C(0,3).
∵B(3,0),
∴OB=OC=3.
∵∠COB=90°,
∴∠OCB=∠BCM=45°.
又∵∠ACB=∠PCB,
∴∠OCB﹣∠ACB=∠BCM﹣∠PCB,即∠OCA=∠PCM.
∴tan∠OCA=![]() =tan∠PCM.
=tan∠PCM.
∴![]() .
.
故设PM=a,MC=3a,PN=3﹣a.
∴P(3a,3﹣a),
将其代入抛物线解析式y=x2﹣4x+3,得(3a)2﹣4(3﹣a)+3=3﹣a.
解得a1=![]() ,a2=0(舍去).
,a2=0(舍去).
∴P(![]() ,
,![]() ).
).
(3)设抛物线平移的距离为m,得y=(x﹣2)2﹣1﹣m.
∴D(2,﹣1﹣m).
如图2,过点D作直线EF∥x轴,交y轴于点E,交PQ延长线于点F,

∵∠OED=∠QFD=∠ODQ=90°,
∴∠EOD+∠ODE=90°,∠ODE+∠QDP=90°.
∴∠EOD=∠QDF.
∴tan∠EOD=tan∠QDF,
∴![]() .
.
∴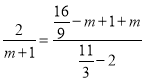 .
.
解得m=![]() .
.
故抛物线平移的距离为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图是某斜拉桥引申出的部分平面图,AE,CD是两条拉索,其中拉索CD与水平桥面BE的夹角为72°,其底端与立柱AB底端的距离BD为4米,两条拉索顶端距离AC为2米,若要使拉索AE与水平桥面的夹角为35°,请计算拉索AE的长.(结果精确到0.1米)(参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,sin72°≈
,sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°≈
,tan72°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在平面直角坐标系xOy中,直线![]() 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线![]() 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
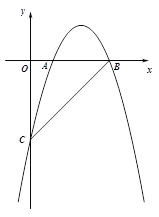


(1)求抛物线的解析式;
(2)点D为线段CB上,点P在对称轴的右侧抛物线上,PD=PB,当tan∠PDB=2,求P点的坐标;
(3)在(2)的条件下,点Q(7,m)在第四象限内,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
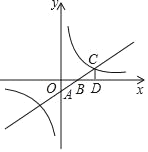
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的表达式;
(2)当x>0时,比较kx+b与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(﹣2,y1),N(﹣1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则y1,y2,y3从小到大的关系是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=![]() x2+bx+c的图象与x轴交于点A(﹣2,0),点B(6,0),与y轴交于点C,顶点为D.
x2+bx+c的图象与x轴交于点A(﹣2,0),点B(6,0),与y轴交于点C,顶点为D.
(1)求抛物线的解析式;
(2)点E是线段AB上的点,直线EM⊥x轴,设点E的横坐标为t.
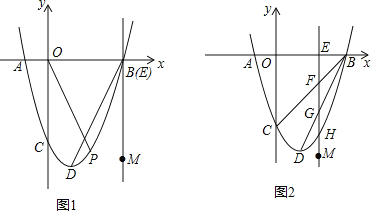
①当t=6时(如图1),点P为x轴下方抛物线上的一点,若∠COP=∠DBM,求此时点P的横坐标;
②当2<t<6时(如图2),直线EM与线段BC,BD和抛物线分别相交于点F,G,H,试证明线段EF,FG,GH总能组成等腰三角形,如果此等腰三角形底角的余弦值为![]() ,求此等腰三角形的面积.
,求此等腰三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 与△DEF 中,下列四个命题是真命题的个数共有( )
①如果A D, ![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
②如果A D,![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
③如果A D 90°,![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
④如果A D 90°, ![]() ,那么△ABC 与△DEF相似.
,那么△ABC 与△DEF相似.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com