
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćAµÄ×ų±źĪŖ£Ø©2£¬2£©£¬µćBµÄ×ų±źĪŖ£Ø6£¬6£©£¬Å×ĪļĻß¾¹żA”¢O”¢BČżµć£¬Į¬½ÓOA”¢OB”¢AB£¬Ļ߶ĪAB½»yÖįÓŚµćE£®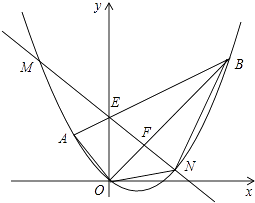
£Ø1£©ĒóµćEµÄ×ų±ź£»
£Ø2£©ĒóÅ×ĪļĻßµÄŗÆŹż½āĪöŹ½£»
£Ø3£©µćFĪŖĻ߶ĪOBÉĻµÄŅ»øö¶Æµć£Ø²»ÓėµćO”¢BÖŲŗĻ£©£¬Ö±ĻßEFÓėÅ×ĪļĻß½»ÓŚM”¢NĮ½µć£ØµćNŌŚyÖįÓŅ²ą£©£¬Į¬½ÓON”¢BN£¬µ±µćFŌŚĻ߶ĪOBÉĻŌĖ¶ÆŹ±£¬Ēó”÷BONĆ껿µÄ×ī“óÖµ£¬²¢Ēó³ö“ĖŹ±µćNµÄ×ų±ź£»
£Ø4£©Į¬½ÓAN£¬µ±”÷BONĆ껿×ī“óŹ±£¬ŌŚ×ų±źĘ½ĆęÄŚĒóŹ¹µĆ”÷BOPÓė”÷OANĻąĖĘ£ØµćB”¢O”¢P·Ö±šÓėµćO”¢A”¢N¶ŌÓ¦£©µÄµćPµÄ×ų±ź£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗÉčÖ±ĻßAB½āĪöŹ½ĪŖy=kx+b£¬
½«A£Ø©2£¬2£©£¬B£Ø6£¬6£©“śČė£¬µĆ ![]() £¬½āµĆ
£¬½āµĆ ![]() £¬
£¬
”ąy= ![]() x+3£¬Įīx=0£¬
x+3£¬Įīx=0£¬
”ąE£Ø0£¬3£©
£Ø2£©
½ā£ŗÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax2+bx+c£¬
½«A£Ø©2£¬2£©£¬B£Ø6£¬6£©£¬O£Ø0£¬0£©Čżµć×ų±ź“śČė£¬µĆ  £¬½āµĆ
£¬½āµĆ  £¬
£¬
”ąy= ![]() x2©
x2© ![]() x
x
£Ø3£©
½ā£ŗŅĄĢāŅā£¬µĆÖ±ĻßOBµÄ½āĪöŹ½ĪŖy=x£¬Éč¹żNµćĒŅÓėÖ±ĻßOBĘ½ŠŠµÄÖ±Ļß½āĪöŹ½ĪŖy=x+m£¬
ĮŖĮ¢  £¬µĆx2©6x©4m=0£¬µ±”÷=36+16m=0Ź±£¬¹żNµćÓėOBĘ½ŠŠµÄÖ±ĻßÓėÅ×ĪļĻßÓŠĪØŅ»µÄ¹«¹²µć£¬ŌņµćNµ½BOµÄ¾ąĄė×ī“ó£¬ĖłŅŌ”÷BONĆ껿×ī“ó£¬
£¬µĆx2©6x©4m=0£¬µ±”÷=36+16m=0Ź±£¬¹żNµćÓėOBĘ½ŠŠµÄÖ±ĻßÓėÅ×ĪļĻßÓŠĪØŅ»µÄ¹«¹²µć£¬ŌņµćNµ½BOµÄ¾ąĄė×ī“ó£¬ĖłŅŌ”÷BONĆ껿×ī“ó£¬
½āµĆm=© ![]() £¬x=3£¬y=
£¬x=3£¬y= ![]() £¬¼“N£Ø3£¬
£¬¼“N£Ø3£¬ ![]() £©£»
£©£»
“ĖŹ±”÷BONĆ껿= ![]() ”Į6”Į6©
”Į6”Į6© ![]() £Ø
£Ø ![]() +6£©”Į3©
+6£©”Į3© ![]() ”Į
”Į ![]() ”Į3=
”Į3= ![]()
£Ø4£©
½ā£ŗ¹żµćA×÷AS”ĶGQÓŚS£¬

”ßA£Ø©2£¬2£©£¬B£Ø6£¬6£©£¬N£Ø3£¬ ![]() £©£¬
£©£¬
”ß”ĻAOE=”ĻOAS=”ĻBOH=45”ć£¬
OG=3£¬NG= ![]() £¬NS=
£¬NS= ![]() £¬AS=5£¬
£¬AS=5£¬
ŌŚRt”÷SANŗĶRt”÷NOGÖŠ£¬
”ątan”ĻSAN=tan”ĻNOG= ![]() £¬
£¬
”ą”ĻSAN=”ĻNOG£¬
”ą”ĻOAS©”ĻSAN=”ĻBOG©”ĻNOG£¬
”ą”ĻOAN=”ĻNOB£¬
”ąONµÄŃÓ³¤ĻßÉĻ“ęŌŚŅ»µćP£¬Ź¹µĆ”÷BOP”×”÷OAN£¬
”ßA£Ø©2£¬2£©£¬N£Ø3£¬ ![]() £©£¬
£©£¬
”ß”÷BOPÓė”÷OANĻąĖĘ£ØµćB”¢O”¢P·Ö±šÓėµćO”¢A”¢N¶ŌÓ¦£©£¬¼“”÷BOP”×”÷OAN£¬
”ąBO£ŗOA=OP£ŗAN=BP£ŗON
ÓÖ”ßA£Ø©2£¬2£©£¬N£Ø3£¬ ![]() £©£¬B£Ø6£¬6£©£¬
£©£¬B£Ø6£¬6£©£¬
”ąBO=6 ![]() £¬OA=2
£¬OA=2 ![]() £¬AN=
£¬AN= ![]() £¬ON=
£¬ON= ![]() £¬
£¬
”ąOP= ![]() £¬BP=
£¬BP= ![]() £¬
£¬
ÉčPµć×ų±źĪŖ£Ø4x£¬x£©£¬
”ą16x2+x2=£Ø ![]() £©2£¬
£©2£¬
½āµĆx= ![]() £¬4x=15£¬
£¬4x=15£¬
”ßP”¢P”ä¹ŲÓŚÖ±Ļßy=xÖį¶Ō³Ę£¬
”ąPµć×ų±źĪŖ£Ø15£¬ ![]() £©»ņ£Ø
£©»ņ£Ø ![]() £¬15£©£®
£¬15£©£®
”¾½āĪö”æ£Ø1£©øł¾ŻA”¢BĮ½µć×ų±źĒóÖ±ĻßABµÄ½āĪöŹ½£¬Įīx=0£¬æÉĒóEµć×ų±ź£»£Ø2£©ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax2+bx+c£¬½«A£Ø©2£¬2£©£¬B£Ø6£¬6£©£¬O£Ø0£¬0£©Čżµć×ų±ź“śČė£¬ĮŠ·½³Ģ×éĒóa”¢b”¢cµÄÖµ¼“æÉ£»£Ø3£©ŅĄĢāŅā£¬µĆÖ±ĻßOBµÄ½āĪöŹ½ĪŖy=x£¬Éč¹żNµćĒŅÓėÖ±ĻßOBĘ½ŠŠµÄÖ±Ļß½āĪöŹ½ĪŖy=x+m£¬ÓėÅ×ĪļĻß½āĪöŹ½ĮŖĮ¢£¬µĆ³ö¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģ£¬µ±”÷=0Ź±£¬”÷BONĆ껿×ī“ó£¬ÓÉ“ĖæÉĒómµÄÖµ¼°NµćµÄ×ų±ź£»£Ø4£©øł¾ŻČż½ĒŠĪĻąĖʵĊŌÖŹµĆµ½BO£ŗOA=OP£ŗAN=BP£ŗON£¬Č»ŗóøł¾Ż¹“¹É¶ØĄķ·Ö±š¼ĘĖć³öBO=6 ![]() £¬OA=2
£¬OA=2 ![]() £¬AN=
£¬AN= ![]() £¬ON=
£¬ON= ![]() £¬ÕāŃłæÉĒó³öOP=
£¬ÕāŃłæÉĒó³öOP= ![]() £¬BP=
£¬BP= ![]() £¬ÉčPµć×ų±źĪŖ£Øx£¬y£©£¬ŌŁĄūÓĆ¹“¹É¶ØĄķµĆµ½¹ŲÓŚx£¬yµÄ·½³Ģ×飬½ā·½³Ģ×鼓æÉ£®
£¬ÉčPµć×ų±źĪŖ£Øx£¬y£©£¬ŌŁĄūÓĆ¹“¹É¶ØĄķµĆµ½¹ŲÓŚx£¬yµÄ·½³Ģ×飬½ā·½³Ģ×鼓æÉ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æA”¢BĮ½µŲĻą¾ą216Ē§Ć×£¬¼×”¢ŅŅ·Ö±šŌŚA”¢BĮ½µŲ£¬Čō¼×Ęļ³µµÄĖŁ¶ČĪŖ15Ē§Ć×/Ź±£¬ŅŅĘļ³µµÄĖŁ¶ČĪŖ12Ē§Ć×/Ź±”£.
£Ø1£©¼×”¢ŅŅĶ¬Ź±³ö·¢£¬±³Ļņ¶ųŠŠ£¬ĪŹ¼øŠ”Ź±ŗóĖūĆĒĻą¾ą351Ē§Ć×£æ
£Ø2£©¼×”¢ŅŅĻąĻņ¶ųŠŠ£¬¼×³ö·¢ČżŠ”Ź±ŗóŅŅ²Å³ö·¢£¬ĪŹŅŅ³ö·¢¼øŠ”Ź±ŗóĮ½ČĖĻąÓö£æ
£Ø3£©¼×”¢ŅŅĻąĻņ¶ųŠŠ£¬ŅŖŹ¹ĖūĆĒĻąÓöÓŚABµÄÖŠµć£¬ŅŅŅŖ±Č¼×ĻČ³ö·¢¼øŠ”Ź±£æ
£Ø4£©¼×”¢ŅŅĶ¬Ź±³ö·¢£¬ĻąĻņ¶ųŠŠ£¬¼×µ½“ļB“¦£¬ŅŅµ½“ļA“¦¶¼·Ö±šĮ¢¼“·µ»Ų£¬¼øŠ”Ź±ŗóĻąÓö£æĻąÓöµŲµć¾ąĄėAÓŠ¶ąŌ¶£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒ¹¤ČĖŹ¦øµÓĆĶ¬Ņ»ÖÖ²ÄĮĻÖĘ³ÉµÄ½šŹōæņ¼Ü£¬ŅŃÖŖ”ĻB£½”ĻE£¬AB£½DE£¬BF£½EC£¬ĘäÖŠ”÷ABCµÄÖܳ¤ĪŖ24cm£¬CF£½3cm£¬ŌņÖĘ³ÉÕūøö½šŹōæņ¼ÜĖłŠčÕāÖÖ²ÄĮĻµÄ×ܳ¤¶ČĪŖ ________cm.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
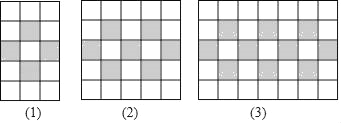
”¾ĢāÄæ”æČēĶ¼£¬Ķ¼°øÓɱ߳¤ĻąµČµÄŗŚ”¢°×Į½É«Õż·½ŠĪ°“Ņ»¶Ø¹ęĀÉĘ“½Ó¶ų³É£¬µŚnøöĶ¼°øÖŠ°×É«Õż·½ŠĪµÄøöŹż±ČŗŚÉ«Õż·½ŠĪµÄøöŹż¶ą_____£®£ØÓĆŗ¬ÓŠnµÄ“śŹżŹ½±ķŹ¾£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCDÖŠ£¬E”¢F·Ö±šĪŖ±ßAB”¢CDµÄÖŠµć£¬BDŹĒ¶Ō½ĒĻߣ¬¹żµćA×÷AG”ĪDB½»CBµÄŃÓ³¤ĻßÓŚµćG£® 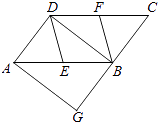
£Ø1£©ĒóÖ¤£ŗDE”ĪBF£»
£Ø2£©Čō”ĻG=90”ć£¬ĒóÖ¤£ŗĖıߊĪDEBFŹĒĮāŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCDÖŠ£¬AB=3£¬AD=4£¬”ĻABC=60”ć£¬¹żBCµÄÖŠµćE×÷EF”ĶAB£¬“¹×ćĪŖµćF£¬ÓėDCµÄŃÓ³¤ĻßĻą½»ÓŚµćH£¬Ōņ”÷DEFµÄĆ껿ŹĒ £® 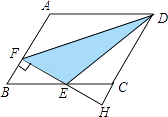
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
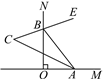
”¾ĢāÄæ”æČēĶ¼£¬”ĻMON£½90”ć£¬µćA£¬B·Ö±šŌŚÉäĻßOM£¬ONÉĻŌĖ¶Æ£¬BEĘ½·Ö”ĻABN£¬BEµÄ·“ĻņŃÓ³¤ĻßÓė”ĻBAOµÄĘ½·ÖĻß½»ÓŚµćC.
(1)µ±µćA£¬BŅʶÆŗ󣬔ĻBAO£½45”揱£¬”ĻC£½________£»
(2)µ±µćA£¬BŅʶÆŗ󣬔ĻBAO£½60”揱£¬”ĻC£½________£»
(3)ÓÉ(1)(2)²ĀĻė”ĻCŹĒ·ńĖęµćA£¬BµÄŅĘ¶Æ¶ų·¢Éś±ä»Æ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾ĢāĀś·Ö7·Ö£©ŌŚŅ»æĆŹ÷µÄ10Ć×øß“¦ÓŠĮ½Ö»ŗļ×Ó£¬Ņ»Ö»ŗļ×ÓÅĄĻĀŹ÷×ßµ½ĄėŹ÷20Ćד¦µÄ³ŲĢĮµÄA“¦”£ĮķŅ»Ö»ÅĄµ½Ź÷¶„DŗóÖ±½ÓŌ¾µ½A“¦£¬¾ąĄėŅŌÖ±Ļß¼ĘĖć£¬Čē¹ūĮ½Ö»ŗļ×ÓĖł¾¹żµÄ¾ąĄėĻąµČ£¬ĒóÕāæĆŹ÷øß”£

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ŠšŹö²¢Ö¤Ć÷Čż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķ£ØÖ¤Ć÷ÓĆĶ¼ 1£©£»
£Ø2£©ČēĶ¼ 2 ŹĒĘß½ĒŠĒŠĪ£¬Ēó”ĻA+”ĻB+”ĻC+”ĻD+”ĻE+”ĻF+”ĻG µÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com