
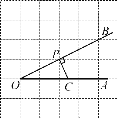
【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到____的距离,____是点C到直线OB的距离.线段PC,PH,OC这三条线段大小关系是___.(用“<”号连接)
科目:初中数学 来源: 题型:
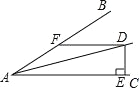
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
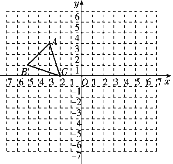
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
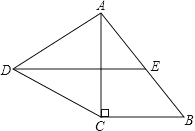
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.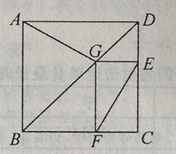
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
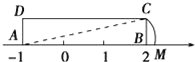
【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
【答案】![]()
【解析】AC=AM=![]() =
=![]() ,∴AM=
,∴AM=![]()
【题型】填空题
【结束】
11
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com