
 如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.分析 (1)连结OD,如图1,根据切线的性质得∠ODE=90°,再证明Rt△OBE≌Rt△ODE得到∠1=∠2,加上∠3=∠C,则利用三角形外角性质可得∠2=∠C,然后根据平行线的判定可判断OE∥AC;
(2)连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,根据等腰三角形的性质和三角形内角和定理,由AB=AC,OC=OD,∠ACB=∠OCD可得∠A=∠COD,根据切线的性质得∠ODE=90°,则∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,利用等角的余角相等得∠ADE=∠DOF,于是有sin∠DOF=sin∠ADE=$\frac{1}{3}$,在Rt△DOF中,根据正弦的定义得到$\frac{DF}{OD}$=$\frac{1}{3}$,则可设DF=x,则OD=3x,利用勾股定理计算出OF=2$\sqrt{2}$x,DF=CF=x,OC=3x,接着可运用面积法计算出DH=$\frac{4\sqrt{2}}{3}$x,然后在Rt△ODH中用勾股定理计算出OH=$\frac{7}{3}$x,再根据正切的定义求解即可.
解答 (1)证明: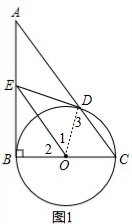 连结OD,如图1,
连结OD,如图1,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△OBE和Rt△ODE中,
$\left\{\begin{array}{l}{OB=OD}\\{OE=OE}\end{array}\right.$,
∴Rt△OBE≌Rt△ODE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠C,
而∠1+∠2=∠C+∠3,
∴∠2=∠C,
∴OE∥AC;
(2)解:连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,
∵AB=AC,OC=OD,
而∠ACB=∠OCD,
∴∠A=∠COD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,
∴∠ADE=∠DOF,
∴sin∠DOF=sin∠ADE=$\frac{1}{3}$,
在Rt△DOF中,sin∠DOF=$\frac{DF}{OD}$=$\frac{1}{3}$,
设DF=x,则OD=3x,
∴OF=$\sqrt{O{D}^{2}-D{F}^{2}}$=2$\sqrt{2}$x,DF=CF=x,OC=3x,
∵$\frac{1}{2}$DH•OC=$\frac{1}{2}$OF•CD,
∴DH=$\frac{2\sqrt{2}x•2x}{3x}$=$\frac{4\sqrt{2}}{3}$x,
在Rt△ODH中,OH=$\sqrt{O{D}^{2}-D{H}^{2}}$=$\frac{7}{3}$x,
∴tan∠DOH=$\frac{DH}{OH}$=$\frac{\frac{4\sqrt{2}}{3}x}{\frac{7}{3}x}$=$\frac{4\sqrt{2}}{7}$,
∴tan∠A=$\frac{4\sqrt{2}}{7}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了解直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | 78分 | B. | 86分 | C. | 80分 | D. | 82分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20、15 | B. | 15、20 | C. | 25、10 | D. | 10、25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 笑笑统计了3月份某天全国8个城市的空气质量指数,并绘制了折线统计图(如图),则这8个城市的空气质量指数的中位数是( )
笑笑统计了3月份某天全国8个城市的空气质量指数,并绘制了折线统计图(如图),则这8个城市的空气质量指数的中位数是( )| A. | 59 | B. | 58 | C. | 50 | D. | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
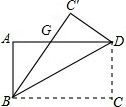 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )| A. | 18.75cm2 | B. | 19.15cm2 | C. | 20cm2 | D. | 21.35cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 是原来的3倍 | B. | 不变 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com