
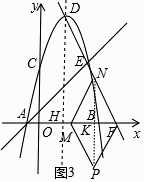
����Ŀ����ͼ1��ʾ����֪������y=��x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬��y�ύ��C�㣬DΪ�����ߵĶ��㣬EΪ��������һ�㣬��C��E���������ߵĶԳ���Գƣ��ֱ���ֱ��AE��DE��
��1����˶��κ����Ĺ�ϵʽ��
��2����ͼ1�У�ֱ��DE����һ��Q��ʹ�á�QCO�ա�QBO�����Q�����ꣻ
��3����ͼ2��ֱ��DE��x�ύ�ڵ�F����MΪ�߶�AF��һ�����㣬��A��F�˶����ٶ�Ϊÿ��2����λ���ȣ��˶���F��ֹͣ����N��F��������������FE�����˶����ٶ�Ϊÿ�� ![]() ����λ���ȣ�M��N����ͬʱ�������˶�ʱ��Ϊt�룬��Mֹͣʱ��Nͬʱֹͣ�˶�����ƽ������һ������P��tΪ��ֵʱ����P��M��N��FΪ������ı����������ƽ���ı��Σ���ֱ��д��tֵ��
����λ���ȣ�M��N����ͬʱ�������˶�ʱ��Ϊt�룬��Mֹͣʱ��Nͬʱֹͣ�˶�����ƽ������һ������P��tΪ��ֵʱ����P��M��N��FΪ������ı����������ƽ���ı��Σ���ֱ��д��tֵ��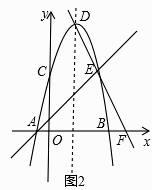
���𰸡�
��1��
�⣺�����ߵĽ���ʽΪy=����x+1����x��5������y=��x2+4x+5��
��2��
�⣺��ͼ1��y=��x2+4x+5=����x��2��2+9����D��2��9���������ߵĶԳ���Ϊֱ��x=2��
��x=0ʱ��y=��x2+4x+5=5����C��0��5����
��C��E���������ߵĶԳ���Գƣ�
��E��4��5����
��ֱ��DE�Ľ���ʽΪy=mx+n��
��D��2��9����E��4��5������� ![]() �����
����� ![]() ��
��
��ֱ��DE�Ľ���ʽΪy=��2x+13��
�ߡ�QCO�ա�QBO��
���COQ=��BOQ��
���QΪ��һ����ƽ�����ϵĵ㣬
��OQ�Ľ���ʽΪy=x��
�ⷽ���� ![]() �����
����� 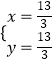 ��
��
��Q��������� ![]() ��
�� ![]() ����
����
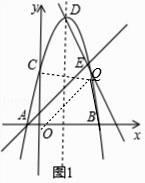
��3��
�⣺��ͼ2��
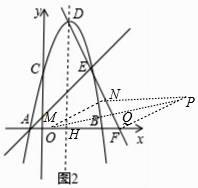
�Գ��ύx���ڵ�H��DH=9��FH= ![]() ��DF=
��DF= ![]() ��
��
��y=0ʱ����2x+13=0�����x= ![]() ����F��
����F�� ![]() ��0����
��0����
��AF= ![]() ������1��=
������1��= ![]() ��
��
AM=2t��FN= ![]() t����FM=
t����FM= ![]() ��2t��
��2t��
����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM���� ![]() t=
t= ![]() ��2t�����t=
��2t�����t= ![]() ��
��
����P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q����PM��NQ���ഹֱƽ�֣�FQ= ![]() t��
t��
�á�FQH�ס�FHD��
��FQ��FH=FM��FD���� ![]() t��
t�� ![]() =��
=�� ![]() ��2t����
��2t���� ![]() �����t=
�����t= ![]() ��
��
����P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3����MF��NP���ഹֱƽ�֣�FK= ![]() MF=
MF= ![]() ��
�� ![]() ��2t����
��2t����
�á�FKN�ס�FHD��
��FK��FH=FN��FD���� ![]() ��
�� ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() �����t=
�����t= ![]() ��
��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬
�á�FMN�ס�FHD��
��FM��FH=FN��FD������ ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() �����t=
�����t= ![]() ��
��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬
�á�FNM�ס�FHD��
��FM��FD=FN��FH������ ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() �����t=
�����t= ![]() ��
��
����������t��ֵΪ ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
����������1��ֱ�����ý���ʽд�������ߵĽ���ʽ����2����ͼ1�������䷽���õ�D��2��9���������ߵĶԳ���Ϊֱ��x=2����ȷ��C��0��5������E��4��5�����������ô���ϵ�������ֱ��DE�Ľ���ʽΪy=��2x+13��Ȼ�����ȫ�������ε����ʵõ���COQ=��BOQ�����Ե�QΪ��һ����ƽ�����ϵĵ㣬���ⷽ���� ![]() ��Q������ꣻ��3����ͼ2���Գ��ύx���ڵ�H����ȷ��DH=9��FH=
��Q������ꣻ��3����ͼ2���Գ��ύx���ڵ�H����ȷ��DH=9��FH= ![]() ��DF=
��DF= ![]() ��AF=
��AF= ![]() ��AM=2t��FN=
��AM=2t��FN= ![]() t����FM=
t����FM= ![]() ��2t���������ۣ�����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����
��2t���������ۣ�����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM���� ![]() t=
t= ![]() ��2t������P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q���������ε����ʵ�FQ=
��2t������P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q���������ε����ʵ�FQ= ![]() t����ͨ���á�FQH�ס�FHD�õ�
t����ͨ���á�FQH�ס�FHD�õ� ![]() t��
t�� ![]() =��
=�� ![]() ��2t����
��2t���� ![]() ������P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3���������ε����ʵ�FK=
������P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3���������ε����ʵ�FK= ![]() ��
�� ![]() ��2t������ͨ����FKN�ס�FHD�õ�
��2t������ͨ����FKN�ס�FHD�õ� ![]() ��
�� ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() ������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬ͨ����FMN�ס�FHD�õ���
������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬ͨ����FMN�ס�FHD�õ��� ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() ������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬ͨ����FNM�ס�FHD�õ���
������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬ͨ����FNM�ס�FHD�õ��� ![]() ��2t����
��2t���� ![]() =
= ![]() t��
t�� ![]() ��Ȼ��ֱ�����t�ķ��̿�ȷ������������t��ֵ��
��Ȼ��ֱ�����t�ķ��̿�ȷ������������t��ֵ��
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij��ѧ�С��ѡ������ɽ������AE�ĸߣ�������30m�ߵ�¥CD�ĵײ���D�������A������Ϊ45�㣬��¥��C�������A������Ϊ36��52�䣮��Сɽ��BE=62m��¥�ĵײ�D��ɽ����ͬһˮƽ���ϣ��������ĸ�AE�����ο����ݣ�sin36��52���0.60��tan36��52���0.75�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����½�Ϊ30���ɽ������һ����AB������ǰ��������һ������ƣ���������ˮƽ�߳�45���ʱ���������AB����б���� ��Ӱ��BD�ij�Ϊ6�ף����ڹ�����ϵ�Ӱ��CD�ij�Ϊ4�ף�������AB�ĸߣ�AB��CD����ˮƽ�洹ֱ������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ���ABD=��CBD=60�㣬AC��BD�ཻ�ڵ�E������C����O�����ߣ���AB���ӳ����ཻ�ڵ�F�� 
��1���жϡ�ACD����״��������֤��
��2����CF=2��DE=4������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������ABCD�У�AC��BD�ǶԽ��ߣ��ֱ��ӳ�AD��E���ӳ�CD��F��ʹ��DE=AD��DF=CD�� 
��1����֤���ı���ACEFΪ���Σ�
��2����ͼ2����E��EG��AC���ӳ�����G����AG=8��cos��ECG= ![]() ����AD= ��ֱ����գ���
����AD= ��ֱ����գ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���3�˾ۻᣬÿ�˴���һ���������3������ֱ����3����ȫ��ͬ�ĺ����ÿ�������ȡһ����У�װ������ĺ��ӣ�
��1�������¼��DZ�Ȼ�¼����� A ��û�г鵽�Լ�����������B ��ǡ�ó鵽�Լ�����������C �ҳ鵽һ������D ֻ���ҳ鵽�Լ�����������
��2���ס��ҡ���3�˳鵽�Ķ������Լ������������Ϊ�¼�A�������г��¼�A�����п��ܵĽ���������¼�A�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A1B1C1D1E1F1�ı߳�Ϊ2����������A2B2C2D2E2F2�����Բ����������A1B1C1D1E1F1�ĸ������У���������A3B3C3D3E3F3�����Բ����������A2B2C2D2E2F2�ĸ������У����������Ĺ��ɽ�����ȥ��A10B10C10D10E10F10�ı߳�Ϊ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У�AB��BC����֪��B=30�㣬AB=![]() ������ABC��AC��������AB��C��ʹ��B������ABCD���ڵ�ƽ���ڣ�����B��D������AB��D��ֱ�������Σ���BC�ij�Ϊ ��
������ABC��AC��������AB��C��ʹ��B������ABCD���ڵ�ƽ���ڣ�����B��D������AB��D��ֱ�������Σ���BC�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1�������ĸ����ۣ�
��b2��4ac����2a+b=0����a+b+c��0��������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2 ��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2 ��
������ȷ�����ǣ�������
A.�ڢ�
B.�٢�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com