
| A. | 1:3:5 | B. | 1:4:9 | C. | 3:6:7 | D. | 6:7:8 |
分析 首先设假山的体积为x,根据第一次是第二次的$\frac{1}{3}$表示出小假山的体积为$\frac{1}{3}$x,再由第三次是第二次的2倍可得小假山和大假山的体积和为2x,进而计算出大假山的体积,然后再计算比值即可.
解答 解:设假山的体积为x,则小假山的体积为$\frac{1}{3}$x,小假山和大假山的体积和为2x,
大假山的体积为2x-$\frac{1}{3}$x=$\frac{5}{3}$x,
三个假山的体体积之比是:$\frac{1}{3}$x:x:$\frac{5}{3}$x=1:3:5,
故选:A.
点评 此题主要考查了代数式求值,关键是正确理解题意,分别表示出三个假山的体积.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
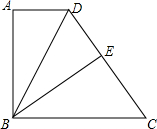 如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.
如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com