
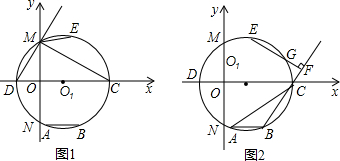
·ÖĪö £Ø1£©øł¾ŻÖ±Ļß½āĪöŹ½½ā³öD£¬M×ų±ź£¬ŌŁøł¾Ż”÷DMO”×”÷DCM£¬ĮŠ±ČĄżŹ½½ā³öŌ²µÄÖ±¾¶³¤£¬Į¬½ÓEO1£¬ĄūÓĆÖ±½ĒČż½ĒŠĪ½ā³öEµć×ų±ź£®
£Ø2£©×÷øØÖśĻߣ¬¹¹½ØÖ±½ĒČż½ĒŠĪ£¬·Ö±š¼ĘĖćMC”¢MDŗĶMEµÄ³¤£¬æÉµĆ½įĀŪ£»
£Ø3£©Į¬½ÓEC£¬¹żE×÷EH”ĶACÓŚH£¬Ź×ĻČÖ¤”ĻECF=”ĻECH£ØæÉĮ¬½ÓEA£¬ĄūÓĆŌ²ÄŚ½ÓĖıߊĪµÄŠŌÖŹĄ“Ē󣩣¬Č»ŗóĶعżÖ¤”÷ECF”¢”÷ECHČ«µČĄ“½ā£¬ŌŁÖ¤Ć÷”÷EAH”Õ”÷EBF£¬øł¾Ż¶ŌÓ¦±ßĻąµČæÉµĆ½įĀŪ£®
½ā“š 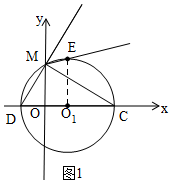 ½ā£ŗ£Ø1£©ČēĶ¼1£¬”ßÖ±ĻßDMµÄ½āĪöŹ½ĪŖy=3x+3£¬
½ā£ŗ£Ø1£©ČēĶ¼1£¬”ßÖ±ĻßDMµÄ½āĪöŹ½ĪŖy=3x+3£¬
”ąD£Ø-1£¬0£©£¬M£Ø0£¬3£©£¬
”ąOD=1£¬OM=3£¬
”ß”÷DMO”×”÷DCM£¬
”ą$\frac{OD}{DM}=\frac{DM}{CD}$£¬
”ąOD•CD=DM•DM£¬DM=$\sqrt{1+9}$=$\sqrt{10}$£¬
”ąCD=$\sqrt{10}•\sqrt{10}$£¬
”ąCD=10£¬°ė¾¶ĪŖ$\frac{1}{2}$CD=5£®
Į¬½ÓEO1£¬Ņ×ÖŖ”ĻEO1C=2”ĻEMC=90”ć£®
”ąµćEµÄ×ų±ź£Ø4£¬5£©£®
£Ø2£©ČēĶ¼2£¬Óɹ“¹É¶ØĄķµĆ£ŗMC=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$£¬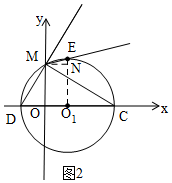
MD=$\sqrt{10}$£¬
¹żM×÷MN”ĶO1EÓŚN£¬ŌņEN=5-3=2£¬MN=4£¬
Óɹ“¹É¶ØĄķµĆ£ŗME=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$£¬
”ą$\sqrt{2}$ME=$\sqrt{2}$”Į$2\sqrt{5}$=2$\sqrt{10}$£¬
”ąMC-MD=3$\sqrt{10}$-$\sqrt{10}$=2$\sqrt{10}$=$\sqrt{2}$ME£»
£Ø3£©ČēĶ¼3£¬Į¬½ÓEC£¬¹żE×÷EH”ĶACÓŚH£¬Į¬½ÓEA”¢EB”¢EC£»
Ó֔ߔĻEO1C=90”ć£¬AB”ĪCD£¬
”ą$\widehat{AD}=\widehat{BC}$£¬
”ą$\widehat{ECB}$=$\widehat{EDN}$£¬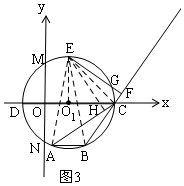
”ą”ĻECH=”ĻEAB
”ßE”¢A”¢B”¢CĖÄµć¹²Ō²£¬
”ą”ĻEAB=”ĻECF£¬
”ą”ĻECH=”ĻECF£¬
ÓÖ”ßEC=EC£¬”ĻEHC=”ĻEFC=90”ć£¬
”ą”÷ECF”Õ”÷ECH£¬µĆ³öCF=CH£¬EH=EF£»
Ó֔ߔĻEAC=”ĻEBC£¬
”ą”÷EAH”Õ”÷EBF£¬
”ąBF=AH£¬
”ąBF+CF=AH+CH=AC£®
µćĘĄ ±¾ĢāŹĒŌ²µÄ×ŪŗĻĢā£¬æ¼²éĮĖČż½ĒŠĪµÄĶā½ÓŌ²£¬Č«µČČż½ĒŠĪµÄÖ¤Ć÷”¢ĖÄµć¹²Ō²µÄŠŌÖŹ”¢Ō²ÖܽĒ¶ØĄķŅŌ¼°Ķ¼ŠĪÓė×ų±źĢŲµćµČÖŖŹ¶£¬²¢ÓėŅ»“ĪŗÆŹżĻą½įŗĻ£¬×ŪŗĻŠŌ½ĻĒ棬ÓČĘäŹĒµŚČżĪŹ£¬×÷øØÖśĻߏĒ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ČżøöÄŚ½ĒĘ½·ÖĻߵĽ»µć | B£® | Čż±ß“¹Ö±Ę½·ÖĻߵĽ»µć | ||
| C£® | ČżĢõøßĻߵĽ»µć | D£® | ČżĢõÖŠĻߵĽ»µć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2 | B£® | -3 | C£® | -7 | D£® | 0 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
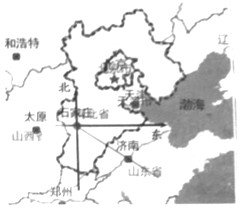 ČēĶ¼£¬¼ĆÄĻ“óŌ¼Ī»ÓŚŹÆ¼Ņ×ƵÄÄĻĘ«¶«56”ć·½ĻņÉĻ£¬ŌņŹÆ¼Ņ×Æ“óŌ¼Ī»ÓŚ¼ĆÄĻµÄ£Ø””””£©
ČēĶ¼£¬¼ĆÄĻ“óŌ¼Ī»ÓŚŹÆ¼Ņ×ƵÄÄĻĘ«¶«56”ć·½ĻņÉĻ£¬ŌņŹÆ¼Ņ×Æ“óŌ¼Ī»ÓŚ¼ĆÄĻµÄ£Ø””””£©| A£® | ±±Ę«Ī÷56”ć·½ĻņÉĻ | B£® | ±±Ę«Ī÷34”ć·½ĻņÉĻ | C£® | ÄĻĘ«Ī÷34”ć·½ĻņÉĻ | D£® | ÄĻĘ«¶«56”ć·½ĻņÉĻ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 Ź«“ŹŹĒĪŅ¹ś¹Å“śĪÄ»ÆÖŠµÄ¹å±¦£¬Ä³ŹŠ½ĢÓżÖ÷¹Ü²æĆÅĪŖĮĖ½ā±¾ŹŠ³õÖŠÉś¶ŌŹ«“ŹµÄѧĻ°Ēéæö£¬¾Ł°ģĮĖŅ»“Ī”°ÖŠ»ŖŹ«“Ź”±±³ĖŠ“óČü£¬Ė껜³éČ”ĮĖ²æ·ÖĶ¬Ń§µÄ³É¼Ø£ØxĪŖÕūŹż£¬×Ü·Ö100·Ö£©£¬»ęÖĘĮĖČēĻĀÉŠ²»ĶźÕūµÄĶ³¼Ę±ķ£®
Ź«“ŹŹĒĪŅ¹ś¹Å“śĪÄ»ÆÖŠµÄ¹å±¦£¬Ä³ŹŠ½ĢÓżÖ÷¹Ü²æĆÅĪŖĮĖ½ā±¾ŹŠ³õÖŠÉś¶ŌŹ«“ŹµÄѧĻ°Ēéæö£¬¾Ł°ģĮĖŅ»“Ī”°ÖŠ»ŖŹ«“Ź”±±³ĖŠ“óČü£¬Ė껜³éČ”ĮĖ²æ·ÖĶ¬Ń§µÄ³É¼Ø£ØxĪŖÕūŹż£¬×Ü·Ö100·Ö£©£¬»ęÖĘĮĖČēĻĀÉŠ²»ĶźÕūµÄĶ³¼Ę±ķ£®| ””×鱚 | ””³É¼Ø·Ö×é£Øµ„Ī»£ŗ·Ö£© | ””ʵŹż | ʵĀŹ”” |
| ””A | ””50”Üx£¼60 | ””40 | ””0.08 |
| ””B | ””60”Üx£¼70 | ””70 | ””0.14 |
| ””C | ””70”Üx£¼80 | ””90 | ””c |
| ””D | ””80”Üx£¼90 | ””a | ””0.40 |
| ””E | ””90”Üx”Ü100 | 100 | 0.20 |
| ””ŗĻ¼Ę | ””b | ””1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® |  | C£® |  | D£® |  |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com