
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:(注:横轴的3应该为5)
(1)乙车休息了 h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)当两车相距40km时,直接写出x的值.
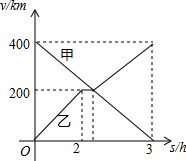
解:(1)设甲车行驶的函数解析式为y甲=kx+b,(k是不为0的常数)
y甲=kx+b图象过点(0,400),(5,0),得
 ,解得
,解得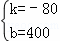 ,
,
甲车行驶的函数解析式为y甲=﹣80x+400,
当y=200时,x=2.5(h),
2.5﹣2=0.5(h),
故答案为0.5;
(2)设乙车与甲车相遇后y乙与x的函数解析式y乙=kx+b,
y乙=kx+b图象过点(2.5,200),(5.400),得
 ,解得
,解得 ,
,
乙车与甲车相遇后y乙与x的函数解析式y乙=80x(2.5≤x≤5);
(3)设乙车与甲车相遇前y乙与x的函数解析式y乙=kx,图象过点(2.5,200),
解得k=80,
∴乙车与甲车相遇后y乙与x的函数解析式y乙=80x,
0≤x≤2.5,y甲减y乙等于40千米,
即400﹣80x﹣100x=40,解得 x=2;
2.5≤x≤5时,y乙减y甲等于40千米,
即2.5≤x≤5时,80x﹣(﹣80x+400)=40,解得x=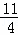 ,
,
综上所述:x=2或x=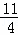 .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
已知梯形ABCD,请使用无刻度直尺画图.
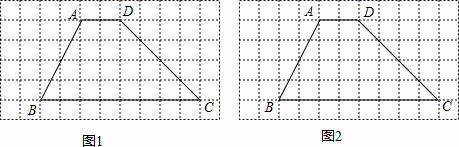
(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校举办“成语听写大赛”,15名学生进入决赛,他们所得分数互不相同,比赛共设8个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是 (填“平均数”或“中位数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(图略),从一副扑克牌中选取红桃10,方块10,梅花5,黑桃8四张扑克牌,洗匀后正面朝下放在桌子上,甲先从中任意抽取一张后,乙再从剩余的三张扑克牌中任意抽取一张,用画树形图或列表的方法,求甲乙两人抽取的扑克牌的点数都是10的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
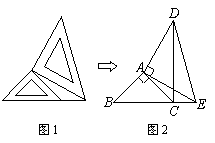
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: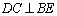 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下表:
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 |
| 2 | 8 | 10 | 17 | 6 | 13 | 7 | 5 | 7 | 3 |
| 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为c级的频率。
(2)试估计1500个18~35岁的青年人中“日均发微博条数”为c级的人数;
(3)从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com