
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
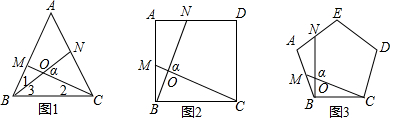
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
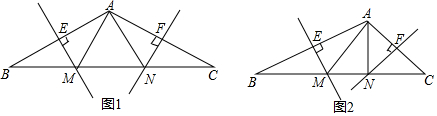
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
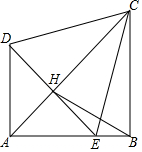 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:| A. | 只有①② | B. | 只有③④ | C. | 只有①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com