练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．实数a，b在数轴上的对应点如图所示，则|a-b|-$\sqrt{a^2}$=b．

    分析 根据数轴得出a＜0＜b，即可知a-b＜0，根据绝对值的性质和二次根式的性质即可化简原式．

    解答 解：由数轴可知a＜0＜b，
    ∴a-b＜0，
    则原式=-（a-b）-（-a）=-a+b+a=b，
    故答案为：b．

    点评 本题主要考查实数和数轴、二次根式的性质和绝对值的性质，熟练掌握二次根式的性质：$\sqrt{{a}^{2}}$=|a|是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．有x支球队参加篮球比赛，共比赛了21场，每两队之间都比赛一场，则下列方程中符合题意的是（　　）
    A．x（x-1）=21B．x（x+1）=21C．x（x-1）=42D．x（x+1）=42

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知直线y-kx+k=0与直线ky+x-2k=0的交点在y轴上，则k的值为（　　）
    A．-2B．2C．-1D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）（-3a2）2×a4-（-5a4）2
    （2）（-2）${\;}^{5}÷（-2）^{3}-{2}^{0}+（-\frac{1}{3}）^{-2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

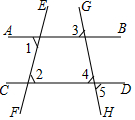    15．如图，已知∠1=∠2，试说明∠3=∠5．请你把说理过程补充完整．
    ∵∠1=∠2（已知）
    ∴AB∥CD（内错角相等，两直线平行）
    ∴∠3=∠4（两直线平行，同位角相等）
    ∵∠4=∠5 （对顶角相等）
    ∴∠3=∠5 （等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．自学：如图1，△ABC中，D是BC边上一点，则△ABD与△ADC有一个相同的高，它们的面积之比等于相应的底之比，记为$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$．
    （△ABD，△ADC的面积分别用记号S△ABD，S△ADC表示）
    心得：如图1，若BD=$\frac{1}{2}$DC，则S△ABD：S△ADC=1：2
    成长：如图2，△ABC中，M，N分别是AB，AC边上一点，且有AM：MB=2：1，AN：NC=1：1，则△AMN与△ABC的面积比为1：3．
    巅峰：如图3，△ABC中，P，Q，R分别是BC，CA，AB边上的点，且AP，BQ，CR相交于点O，现已知△BPO，△PCO，△COQ，△AOR的面积依次为40，30，35，84，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某校为开展体育大课间活动，需要购买篮球与足球若干个．已知购买2个篮球和3个足球共需要380元；购买4个篮球和5个足球共需要700元．
    （1）求购买一个篮球、一个足球各需多少元？
    （2）若体育老师带了6000元去购买这种篮球与足球共80个．由于数量较多，店主给出“一律打九折”的优惠价，那么他最多能购买多少个篮球？

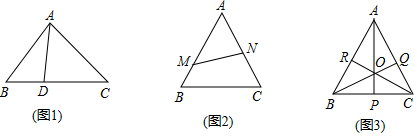
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在下列调查中，适宜采用普查的是（　　）
    A．对我省七年级学生视力情况的调查
    B．对一批LED节能灯使用寿命的调查
    C．对量子通信卫星上零部件质量的调查
    D．对“最强大脑”节目收视率的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点

    （1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．
    （2）当点P在C、D两点的外侧运动时（P点与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．

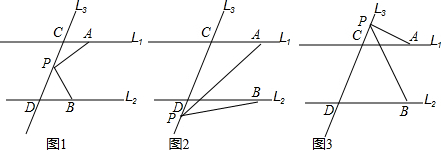
    查看答案和解析>>

    同步练习册答案