
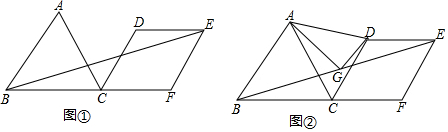
分析 (1)如图1,作高线EH,利用平行线的性质得:∠FEH=30°,则FH=$\frac{1}{2}EF=4$,利用勾股定理求EH的长,利用三角形面积公式求面积即可;
(2)如图2,作辅助线,构建全等三角形,先证△BGM≌△EGD,则BM=ED=CD,MG=DG,再证明△ABM≌△ACD,则∠BAM=∠CAD,AM=AD,所以△MAD是等边三角形,由三线合一可得结论.
解答  解:(1)如图1,∵等边△ABC,
解:(1)如图1,∵等边△ABC,
∴BC=AB=10,∠ABC=60°,
∵AB∥CD,
菱形DCFE中,DC∥EF,
∴AB∥EF,
∴∠EFH=∠ABC=60°,
∵EH⊥CF
∴∠FEH=30°
∴FH=$\frac{1}{2}EF=4$,
∴EH=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵菱形CFED,EF=8,
∴CF=EF=8,
∴BF=BC+EF=18,
∴${S_{△BFE}}=\frac{1}{2}BF•EH=\frac{1}{2}×18×4\sqrt{3}=36\sqrt{3}$;
(2)AG⊥GD,AG=$\sqrt{3}$DG; 
理由如下:
如图2,延长DG与BC交于M,连接AM,
∵四边形CDEF是菱形,
∴DE=DC,DE∥CF,
∴∠GBM=∠GED,∠GMB=∠GDE,
∵G是BC的中点,
∴BG=EG,
在△BGH和△EGD中,
∴△BGM≌△EGD(AAS),
∴BM=ED=CD,MG=DG,
∵等边△ABC中,
∴∠ABC=∠ACB=60°,
又∵AB∥CD
∴∠DCF=∠ABC=60°,
∴∠ACD=180°-(∠ACB+∠DCF)=60°,
∴∠ABC=∠ACD,
在△ABH和△ACD中,
∵$\left\{{\begin{array}{l}{AB=AC}\\{∠ABC=∠ACD}\\{BM=CD}\end{array}}\right.$,
∴△ABM≌△ACD(SAS),
∴∠BAM=∠CAD,AM=AD,
∴∠MAD=∠BAC=60°;
∵AD=AM,MG=DG,
∴△MAD是等边三角形,
∴AG⊥MD,∠MAG=∠DAG=30°,
∴AG:DG=$\sqrt{3}:1$,
∴AG=$\sqrt{3}$DG.
点评 本题是四边形的综合题,难度适中,考查了菱形的性质、等边三角形的性质和判定、等腰三角形的三线合一的性质、三角形全等的性质和判定等知识,第二问是常考题型,构建辅助线,证明△AMD是等腰三角形是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调入地 水量/万吨 调出地 | C | D |
| A | x | 200-x |
| B | 240-x | 60+x |
| 总计 | 240 | 260 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
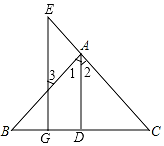 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com