Question

3．问题：如图1，在Rt△ABC中，∠C=90°，∠ABC=30°，点D是边CB上任意一点，△ADE是等边三角形，且点E在∠ACB的内部，连接BE．探究线段BE与DE之间的数量关系，请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
（1）当点D与点C重合时（如图2），请你补全图形．由∠BAC的度数为60°，点E落在AB中点处，容易得出BE与DE之间的数量关系为BE=DE；
（2）当点D是BC上任意一点（不与点B，C重合）时，结合图1，研究（1）中线段BE与DE之间的数量关系是否与成立，并证明你的结论；
（3）如图3，在直线BC上有一点P，使△PAB为等腰三角形，请找出这样的点P，并直接写出∠APB的度数．

Answer 1

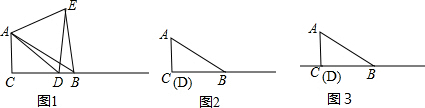
分析 （1）根据题意画出图形，由直角三角形及等边三角形的性质即可得出结论；
（2）根据题意画出图形，猜想：BE=DE，取AB的中点F，连接EF，由∠ACB=90°，∠ABC=30°，可知∠1=60°，CF=AF=$\frac{1}{2}$AB，故△ACF是等边三角形，再由△ADE是等边三角形可得出∠CAD=∠FAE，由全等三角形的判定定理可知△ACD≌△AFE，故∠ACD=∠AFE=90°．由F是AB的中点，可知EF是AB的垂直平分线，进而可得出△ADE是等边三角形，故DE=AE，BE=DE；
（3）分三种情况讨论计算即可．

解答 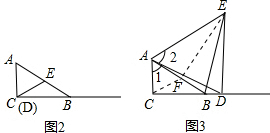解：（1）如图2，
∵∠C=90°，∠ABC=30°，
∴∠BAC=60°，
∵△ADE是等边三角形，
∴AE=CE，
∴点E落在AB的中点处；
∴AE=CE=BE=DE，
故答案为：60°；AB的中点处；BE=DE；

（2）如图3．
猜想：BE=DE．
证明：取AB的中点F，连接EF．
∵∠ACB=90°，∠ABC=30°，
∴∠1=60°，CF=AF=$\frac{1}{2}$AB，
∴△ACF是等边三角形．
∴AC=AF　  ①
∵△ADE是等边三角形，
∴∠2=60°，AD=AE   ②
∴∠1=∠2．
∴∠1+∠BAD=∠2+∠BAD．
即∠CAD=∠FAE③
由①②③得△ACD≌△AFE（SAS）． 
∴∠ACD=∠AFE=90°．
∵F是AB的中点，
∴EF是AB的垂直平分线，
∴BE=AE，
∵△ADE是等边三角形，
∴DE=AE，
∴BE=DE；
（3）如图4，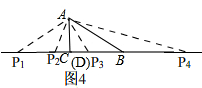
∵△PAB为等腰三角形，
∴①当AP=AB时，即：AP₁=AB，
∴∠AP₁B=∠ABP₁=30°，
②当BP=AB时，
Ⅰ、BP₂=AB，
∴∠AP₂B=$\frac{1}{2}$（180°-∠ABC）=75°，
Ⅱ、BP₄=AB，
∴∠BAP₄=∠AP₄B
∵∠ABC=30°=∠BAP₄+∠AP₄B
∴∠AP₄B=15°
③当AP=BP时，即：AP₃=BP₃，
∴∠BAP₃=∠ABC=30°，
∴∠AP₃B=180°-∠ABC-∠BAP₃=120°，
即：∠APB的度数为15°，30°，75°，120°．

点评 本题是三角形综合题，主要考查的是等边三角形的性质等腰三角形的性质及直角三角形的性质、全等三角形的判定与性质，根据题意画出图形，利用数形结合求解是解答此题的关键．