Question

15．如图，点P是正方形ABCD内的一点，BE=BP，∠EBP=90°，PA=2．PB=$\sqrt{3}$，PC=$\sqrt{10}$．
（1）求证：AE=CP；
（2）求∠APB的度数．

Answer 1

分析 （1）由正方形的性质得出∠ABC=90°，AB=BC，证出∠ABE=∠CBP，由SAS证明△ABE≌△CBP，得出对应边相等即可；
（2）作PM⊥AE于M，由全等三角形的性质证出四边形BPME是矩形，得出∠BPM=90°，PM=BE=BP=$\sqrt{3}$，由勾股定理求出AM=1=$\frac{1}{2}$PA，得出∠APM=30°，即可得出∠APB的度数．

解答 （1）证明：∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC，
∵∠EBP=90°，
∴∠ABE=∠CBP，
在△ABE和△CBP中，$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABE=∠CBP}&{\;}\\{BE=BP}&{\;}\end{array}\right.$，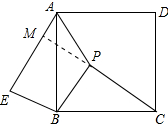
∴△ABE≌△CBP（SAS），
∴AE=CP；
（2）解：作PM⊥AE于M，如图所示：
∵∠BPC=90°，△ABE≌△CBP，
∴∠E=90°，
∵∠EBP=90°，
∴四边形BPME是矩形，
∴∠BPM=90°，PM=BE=BP=$\sqrt{3}$，
∴AM=$\sqrt{P{A}^{2}-P{M}^{2}}$=1=$\frac{1}{2}$PA，
∴∠APM=30°，
∴∠APB=30°+90°=120°．

点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理、矩形的判定与性质等知识；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．