练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    等边三角形的性质
    （1）等边三角形的三个内角都
    相等
    相等
    ，并且每一个角都等于
    60°
    60°
    ．
    （2）等边三角形是轴对称图形，共有
    三
    三
    条对称轴．
    （3）等边三角形每边上的
    中线
    中线
    、
    高线
    高线
    和该边所对内角的平分线互相重合．
    分析：（1）根据等边三角形性质中内角度数进而填空得出；
    （2）利用轴对称图形的性质得出即可；
    （3）根据等腰三角形性质三线合一的性质可得出．
    解答：解：（1）等边三角形的三个内角都相等，并且每一个角都等于60°；

    （2）等边三角形是轴对称图形，它有三条对称轴；

    （3）等边三角形每边上的中线、高线和该边所对内角的平分线互相重合．
    故答案为：（1）相等，60°；（2）三；（3）中线，高线．
    点评：此题主要考查了等三角形的性质，熟练掌握其性质是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图所示，AB为⊙O的直径，P为AB延长线上一点，PD切⊙O于C，BC和AD的延长线相交于点E，且AB=AE。 (1)求证：(2)若圆的半径为1，△ABE是等边三角形，求BP的长．

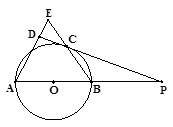
    【解析】（1）连OC，根据切线的性质得到OC⊥PD，又AB=AE，OC=OB，则∠2=∠E，∠1=∠2，得到∠1=∠E，则OC∥AE，即可得到结论；

    （2）根据等边三角形的性质得∠A=60°，则∠COB=60°，则∠P=30°，再根据含30°的直角三角形三边的关系得到OP=2OC=2，从而求出BP

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠BAC＝30º，EF⊥AB，垂足为F，连结DF．

    （1）求证：AC＝EF；

    （2）求证：四边形ADFE是平行四边形．

    【解析】由等边△ABE和Rt△ABC，求得Rt△ABC∽Rt△EAF，即可得AC＝EF，由等边三角形的性质得出∠BDF=30°，从而证得△DBF≌△EFA，则AE=DF，再由FE=AB，得出四边形ADFE为平行四边形

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省泰州市靖江外国语学校中考二模数学卷（解析版） 题型：解答题

    如图所示，AB为⊙O的直径，P为AB延长线上一点，PD切⊙O于C，BC和AD的延长线相交于点E，且AB=AE。 (1)求证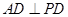： (2)若圆的半径为1，△ABE是等边三角形，求BP的长．

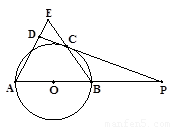
    【解析】（1）连OC，根据切线的性质得到OC⊥PD，又AB=AE，OC=OB，则∠2=∠E，∠1=∠2，得到∠1=∠E，则OC∥AE，即可得到结论；

    （2）根据等边三角形的性质得∠A=60°，则∠COB=60°，则∠P=30°，再根据含30°的直角三角形三边的关系得到OP=2OC=2，从而求出BP

     

    查看答案和解析>>

    科目：初中数学 来源：2012届北京市西城区九年级一模数学卷（解析版） 题型：解答题

    如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠BAC＝30º，EF⊥AB，垂足为F，连结DF．

    （1）求证：AC＝EF；

    （2）求证：四边形ADFE是平行四边形．

    【解析】由等边△ABE和Rt△ABC，求得Rt△ABC∽Rt△EAF，即可得AC＝EF，由等边三角形的性质得出∠BDF=30°，从而证得△DBF≌△EFA，则AE=DF，再由FE=AB，得出四边形ADFE为平行四边形

     

    查看答案和解析>>

    同步练习册答案