
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

【答案】(1)45°(2)![]() (3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
(3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
【解析】(1)先求出∠MOC的度数:(90+30)÷2=60°,∠CON的度数是:30÷2=15°,然后用∠MOC的度数减去∠CON的度数即可得出∠MON的度数.
(2)根据问题(1)的解题思路把∠AOB的度数用字母a代替即可.
(3)根据问题(1)的解题思路把∠BOC的度数用字母![]() 代替即可.
代替即可.
(4)根据(1)(2)(3)的得数可知:∠MON的度数是始终是∠AOB的度数的一半》
解:(1)因为OM平分∠AOC,
所以∠MOC=![]() ∠AOC.
∠AOC.
又因为ON平分∠BOC,
所以∠NOC=![]() ∠BOC.
∠BOC.
所以∠MON=∠MOC-∠NOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB.
∠AOB.
又因为∠AOB=90°,所以∠MON=45°.
(2)当∠AOB=α,其他条件不变时,∠MON=![]() .
.
(3)当∠BOC=β,其他条件不变时,∠MON=45°.
(4)分析(1)(2)(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
“点睛”本题考查了组合角中某个角的度数的求解,根据是明确各角之间的联系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下面几种说法:①对角线互相垂直的四边形是菱形;②一组对边平行,一组邻边相等的四边形是菱形;③对角线相等的平行四边形是矩形;④对角线互相垂直平分的四边形是菱形,那么准确的说法是( )
A.①②③B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分11分)让我们一起探索有趣的“皮克定理”:用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
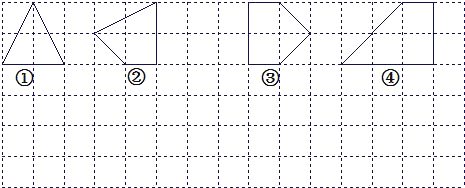 .
.
(1)上图中的格点多边形,其内部都只有一个格点,请完成下表,并写出S与x之间的关系式:S=______.

(2)探索:在上面网格图中画出四个格点多边形,其内部都只有两个格点,并写出所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式:S=______;
(3)猜想:当格点多边形内部有且只有n个格点时,S与x之间的关系式是:S=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com