
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 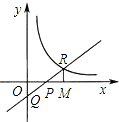
【答案】2 ![]()
【解析】解:∵y=kx﹣2,
∴当x=0时,y=﹣2,
当y=0时,kx﹣2=0,解得x= ![]() ,
,
所以点P( ![]() ,0),点Q(0,﹣2),
,0),点Q(0,﹣2),
所以OP= ![]() ,OQ=2,
,OQ=2,
∵RM⊥x轴,
∴△OPQ∽△MPR,
∵△OPQ与△PRM的面积相等,
∴△OPQ与△PRM的相似比为1,即△OPQ≌△MPR,
∴OM=2OP= ![]() ,RM=OQ=2,
,RM=OQ=2,
所以点R( ![]() ,2),
,2),
∵双曲线 ![]() 经过点R,
经过点R,
∴ ![]() =2,即k2=8,
=2,即k2=8,
解得k1=2 ![]() ,k2=﹣2
,k2=﹣2 ![]() (舍去).
(舍去).
所以答案是:2 ![]() .
.
【考点精析】根据题目的已知条件,利用反比例函数的性质和相似三角形的性质的相关知识可以得到问题的答案,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;对应角相等,对应边成比例的两个三角形叫做相似三角形.


科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC
(1)如图1,判断△BCE的形状,并说明理由; 
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 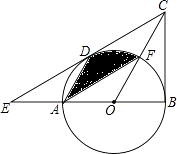
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,△ABO的顶点坐标分别为O(0,0)、A(2a,0)、B(0,﹣a),线段EF两端点坐标为E(﹣m,a+1),F(﹣m,1)(2a>m>a);直线l∥y轴交x轴于P(a,0),且线段EF与CD关于y轴对称,线段CD与NM关于直线l对称.
(1)求点N、M的坐标(用含m、a的代数式表示);
(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明其理由,若能请你说出一个平移方案(平移的单位数用m、a表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
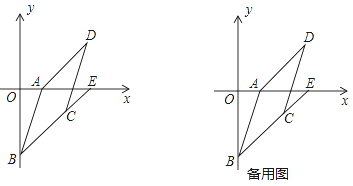
【题目】如图,在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移得到BC,使B(0,b),且a,b满足|a﹣2|+![]() =0,延长BC交x轴于点E.
=0,延长BC交x轴于点E.
(1)填空:点A( , ),点B( , ),∠DAE= ;
(2)求点C和点E的坐标;
(3)设点P是x轴上的一动点(不与点A、E重合),且PA>AE,探究∠APC与∠PCB的数量关系?写出你的结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 .
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 . 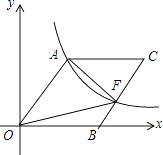
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). 
(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
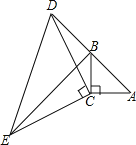
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=2cm,则BE=_______cm.
(3)BE与AD有何位置关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com