
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

【答案】①②④
【解析】
易证△ABD≌△EBC,可得∠BCE=∠BDA,AD=EC可得①②正确,再根据角平分线的性质可求得∠DAE=∠DCE,即AD=AE=EC,根据AD=AE=EC可求得④正确
解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,
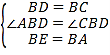 ,
,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∵BD为△ABC的角平分线,EF⊥AB,而EC不垂直与BC,
∴EF≠EC,
∴③错误;
④过E作EG⊥BC于G点,
∵E是BD上的点,∴EF=EG,
在Rt△BEG和Rt△BEF中,
![]() ,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
![]() ,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF,
∴④正确.
故答案为:①②④.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
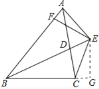
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点![]() 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米![]() 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动![]() 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米![]() 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )
A. 2.5 B. 3 C. 2.25或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将![]() 沿直线BC方向平移
沿直线BC方向平移![]() 的位置,G是DE上一点,连接AG,过点A、D作直线MN.
的位置,G是DE上一点,连接AG,过点A、D作直线MN.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断AG与DE的位置关系,并证明你的结论.
,判断AG与DE的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的数阵是由77个偶数排成:
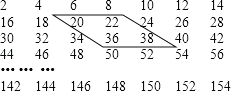
(1)如图中任意作一个平行四边形框,设左上角的数为x,那么其他3个数从小到大可分别表示为 .
(2)小红说这4个数的和是292,能求出这4个数吗?若存在,请求出这4个数.不存在说明理由.
(3)小明说4个数的和是420,存在这样的数吗?若存在,请求出这4个数,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
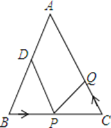
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作![]() ,与AC、DC分别交于点
,与AC、DC分别交于点![]() 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、![]() 下列结论:
下列结论: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,则
,则![]() 其中结论正确的有
其中结论正确的有![]()
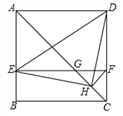
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为2014(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
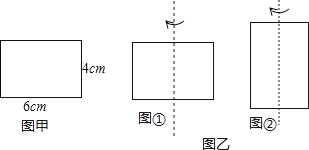
【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 . 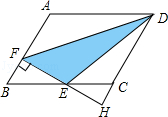
查看答案和解析>>
科目:初中数学 来源: 题型:
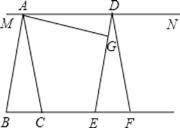
【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
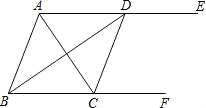
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com