
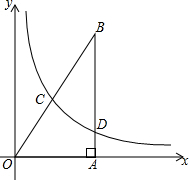
 如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$.
如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$. 分析 如果以B、C、D为顶点的三角形与△OAB相似,则CD⊥BC,根据OA=2,AB=4,求得B(2,4),求出直线BC和AB的解析式,与反比例函数的解析式联立方程组,求出点C.D的坐标,求出直线CD的解析式,再根据两直线垂直斜率的积等于-1列方程即可求得结果.
解答 解:如果以B、C、D为顶点的三角形与△OAB相似,则CD⊥BC,
∵OA=2,AB=4,
∴B(2,4),
设直线OB的解析式为:y=kx,
则4=2k,
∴k=2,
∴直线OB的解析式为:y=2x,
∵AB⊥x轴,
∴直线AB的解析式为:x=2,
解$\left\{\begin{array}{l}{y=2x}\\{y=\frac{k}{x}}\end{array}\right.$与$\left\{\begin{array}{l}{x=2}\\{y=\frac{k}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{\sqrt{2k}}{2}}\\{y=\sqrt{2k}}\end{array}\right.$与$\left\{\begin{array}{l}{x=2}\\{y=\frac{k}{2}}\end{array}\right.$,
∴C($\frac{\sqrt{2k}}{2}$,$\sqrt{2k}$),D(2,$\frac{k}{2}$),
∴直线CD的解析式为:y=$\frac{\sqrt{2k}-\frac{k}{2}}{\frac{\sqrt{2k}}{2}-2}$x+$\frac{2\sqrt{2k}-k}{\frac{\sqrt{2k}}{2}-2}$,
∵CD⊥OB,
∴$\frac{\sqrt{2k}-\frac{k}{2}}{\frac{\sqrt{2k}}{2}-2}$×2=-1,
解得:k=8或k=$\frac{1}{2}$.
当k=8时,反比例函数的图象经过点B(2,4),不符合题意,
故答案为:$\frac{1}{2}$.
点评 本题考查了相似三角形的性质,待定系数法求函数的解析式,求图象的交点坐标,解方程组,知道根据两直线垂直斜率的积等于-1列方程是解题的关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{-3}=-\root{3}{-3}$ | B. | $\root{3}{-3}=\root{3}{3}$ | C. | $\root{3}{-3}=\root{3}{{|{-3}|}}$ | D. | $\root{3}{-3}=-\root{3}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
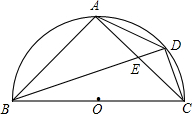 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
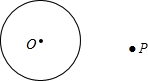 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com