

分析 (1)根据“乘公交”的频数、频率可得总人数,依据:$\frac{频数}{总数}$=频率可分别求得m、n的值;
(2)由(1)可得“骑自行车”的人数,补全条形图即可;
(3)用样本中“骑自行车”所占百分比乘以总人数1500即可.
解答 解:(1)被调查的学生共有:20÷0.4=50(人),
∴m=$\frac{13}{50}$=0.26,n=0.2×50=10;
(2)由(1)知,“骑自行车”的学生有10人,补全条形图如图: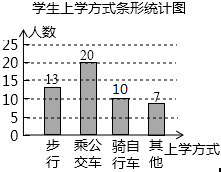
(3)1500×20%=300(人).
答:该校骑自行车上学的学生约有300人.
故答案为:(1)0.26,10.
点评 本题考查的是条形统计图和频数分布表的综合运用,熟练掌握频数分布表中$\frac{频数}{总数}$=频率及条形统计图中每个项目的数据是解题的关键;


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
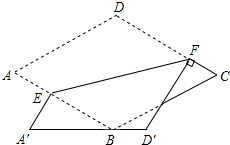 如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.
如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
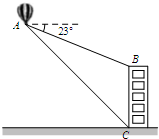 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$.
如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点A,若AM:MN=2:3,则k=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com