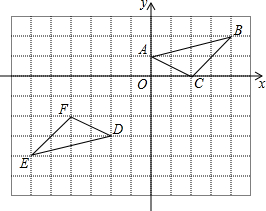
如图.在平面直角坐标系中.点A的坐标为.C的坐标为(2.0).将△ABC绕点P旋转180°得到△DEF.则旋转中心P点的坐标为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

4．

如图，在平面直角坐标系中，点A的坐标为（0，1），点B的坐标为（4，2），C的坐标为（2，0），将△ABC绕点P旋转180°得到△DEF，则旋转中心P点的坐标为（-1，-1）．

分析首先找出两个三角形的对应点，然后连接任意两组对应点，两条线段的交点即为点P的位置．

解答解：连接AD，CF交点为P．

根据图形可知点P的坐标为（-1，-1）．
∴旋转中心P点的坐标为（-1，-1）．

点评本题主要考查的是旋转图形的性质，明确中心对称图形的对应点的连线经过对称中心是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

8．已知P₁（-2，y₁），P₂（-1，y₂）是正比例函数y=-x的图象上的两点，则y₁＞y₂（填“＞”或“＜”或“=”）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．

如图，直线l上有三个正方形A、B、C，若正方形A、C的面积分别为5和11，则正方形B的面积为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

6．

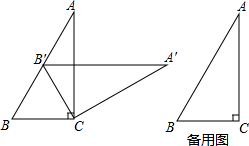
如图，将△ABC的边AB延长2倍至点A₁，边BC延长2倍至点B₁，边CA延长2倍至点C₁，顺次连结A₁、B₁、C₁，得△A₁B₁C₁，再分别延长△A₁B₁C₁的各边2倍得△A₂B₂C₂，…，依次这样下去，得△A_nB_nC_n，若△ABC的面积为1，则△A_nB_nC_n的面积为19ⁿ．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

如图，已知OA⊥OB，OC⊥OD，垂足均为点O．求∠BOC+∠AOD的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

9．

如图，Rt△ABC中AB=6，AC=10，△ABC的内切圆交AC于点D，点P从D出发，沿射线DC每次前进一个单位，点Q从D出发沿DA和射线AB每次前进a个单位，a为正整数且1≤a≤8，当t次前进后△APQ与△ABC相似，所有满足条件的t为1、2、8、16、32．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．在Rt△ABC中，∠C=90°，以三边为边分别向外作正方形，如图所示，过C作CH⊥AB于H，延长CH交MN于点I．
（1）如图（1）若AC=3$\sqrt{2}$，BC=2$\sqrt{3}$，试通过计算证明：四边形AHIN的面积等于正方形AEFC的面积．
（2）请利用图（2）证明直角三角形勾股定理：AC²+BC²=AB²．

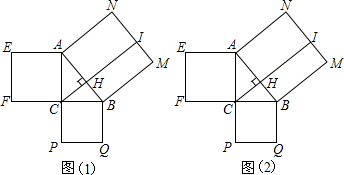
查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．△ABC中，∠ACB=90°，∠A=30°，AC=$\sqrt{3}$，将△ABC绕点C顺时针旋转α，
（1）当点B的对应点B′恰好落在AB边上时（如图），α=60°；
（2）在（1）的条件下，将旋转后的图形沿射线CB平移，设平移的距离为x，平移后的图形与△ABC重叠部分的面积为y，求y与x的函数关系式，并直接写出x的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

自从2012年12月4日中央公布“八项规定”以来，我市某中学积极开展“厉行勤俭节约，反对铺张浪费”的活动．为此，校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查，调查内容分为四种：A．饭和菜全部吃完；B．有剩饭但菜吃完；C．饭吃完但菜有剩；D．饭和菜都有剩．学生会根据统计结果绘制了如下统计表和统计图，根据所提供的信息回答下列问题：

选项	频数	频率
A	30	M
B	n	0.2
C	5	0.1
D	5	0.1

（1）这次被抽查的学生有多少人？
（2）求表中m，n的值，并补全条形统计图；
（3）该中学有学生2200名，请估计这餐晚饭有剩饭的学生人数，按平均每人剩10克米饭计算，这餐晚饭将浪费多少千克米饭？

查看答案和解析>>

同步练习册答案