
【题目】一个透明的布袋里装有2个红球,![]() 个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为
个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)先任意摸出1个球,记下颜色后不放回,搅匀,再摸出一个球,请利用画树状图或列表的方法求出连续两次都摸出红球的概率.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
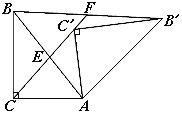
【题目】如图,Rt△ABC中,∠ACB=90°,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
(1)证明:△AC C′∽△AB B′;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时AC=BF,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
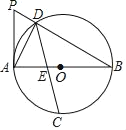
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
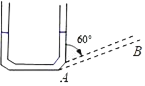
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2+(2m+1)x+m2﹣1=0.
(1)若方程有两个不相等的实数根,试求m的取值范围;
(2)若抛物线y=x2+(2m+1)x+m2﹣1与直线y=x+m没有交点,试求m的取值范围;
(3)求证:不论m取何值,抛物线y=x2+(2m+1)x+m2﹣1图象的顶点都在一条定直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
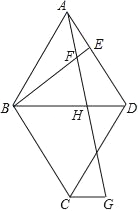
【题目】如图,菱形ABCD中,∠BAD=60°,点E在边AD上,连接BE,在BE上取点F,连接AF并延长交BD于H,且∠AFE=60°,过C作CG∥BD,直线CG、AF交于G.
(1)求证:∠FAE=∠EBA;
(2)求证:AH=BE;
(3)若AE=3,BH=5,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
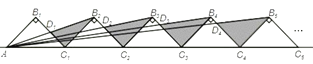
【题目】如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1Dnn的面积为Sn,则S1=_____;S2=_____;Sn=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com