
【题目】有一家苗圃计划种植桃树和柏树.根据市场调查与预测,种植桃树的利润y1(万元)与投资成本x(万元)满足如图①所示的二次函数y1=ax2;种植柏树的利润y2(万元)与投资成本x(万元)满足如图②所示的正比例函数y2=kx.
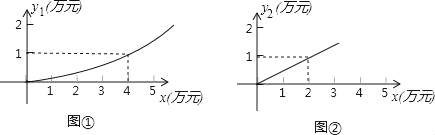
(1)分别求出利润y1(万元)和利润y2(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃投入10万元资金种植桃树和柏树,苗圃至少能获得多少利润?若要使这家苗圃获得5万元利润,资金投入如何分配(桃树和柏树都要种植)?
【答案】(1)y2=![]() x (2)4万 投入8万元种植桃树,投入2万元种植柏树.
x (2)4万 投入8万元种植桃树,投入2万元种植柏树.
【解析】【试题分析】(1)将(4,1)代入y1=ax2,求a即可;将(2,1)代入y2=kx即可;(2)设种植桃树的资金投入为x万元,两项投入所获得的总利润为y万元,则种植柏树的资金投入为(10﹣x) 万元,根据题意得:y=![]() x2+
x2+![]() (10﹣x)=
(10﹣x)=![]() (x﹣4)2+4.
(x﹣4)2+4.
根据二次函数的性质,得:a=![]() >0,则抛物线的开口向上,
>0,则抛物线的开口向上,
故:当x=4时,y有最小值,y最小=4万元.
当![]() (x﹣4)2+4=5时,
(x﹣4)2+4=5时,
解得:x1=8,x2=0(不合题意,舍去).
则10﹣x=10﹣8=2.
从而得解.
【试题解析】
(1)∵抛物线y1=ax2经过点(4,1),
∴42×a=1,解得:a=![]() ,
,
∴y1关于x的函数关系式为y1=![]() x2.
x2.
∵y2=kx经过点(2,1),
∴2k=1,解得k=![]() ,
,
∴y2关于x的函数关系式为y2=![]() x.
x.
(2)设种植桃树的资金投入为x万元,两项投入所获得的总利润为y万元,则种植柏树的资金投入为(10﹣x) 万元,
根据题意得:y=![]() x2+
x2+![]() (10﹣x)=
(10﹣x)=![]() (x﹣4)2+4.
(x﹣4)2+4.
∵a=![]() >0,
>0,
∴抛物线的开口向上,
∴当x=4时,y有最小值,y最小=4万元.
当![]() (x﹣4)2+4=5时,
(x﹣4)2+4=5时,
解得:x1=8,x2=0(不合题意,舍去).
∴10﹣x=10﹣8=2.
答:苗圃至少获得4万元利润;若要使这家苗圃获得5万元利润,要投入8万元种植桃树,投入2万元种植柏树.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
产品资源 | 甲 | 乙 |
矿石(吨) | 10 | 4 |
煤(吨) | 4 | 8 |
生产1吨甲产品所需成本费用为4000元,每吨售价4600元;
生产1吨乙产品所需成本费用为4500元,每吨售价5500元,
现将该矿石原料全部用完,设生产甲产品x吨,乙产品m吨,公司获得的总利润为y元.
(1)写出m与x之间的关系式
(2)写出y与x之间的函数表达式,并写出自变量的范围
(3)若用煤不超过200吨,生产甲产品多少吨时,公司获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
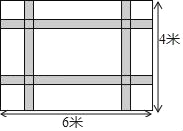
【题目】如图,一块长6米宽4米的地毯,为了美观设计了两横两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.(供参考数据:1052=11025,1152=13225,1252=15625)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.

(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
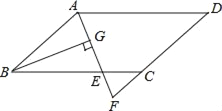
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学在计算![]() 时,将“
时,将“![]() ”错看成了“
”错看成了“![]() ”,得出的结果是
”,得出的结果是![]() .
.
(1)请你求出这道题的正确结果;
(2)试探索:当字母![]() 、
、![]() 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母![]() 的取值无关.
的取值无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,3).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,3).
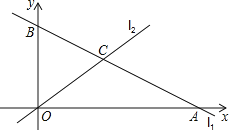
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com