
 гкЕуCЃЌЖЅЕуЮЊPЃЌДЫХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=1ЃЌЧвSЁїAOCЃКSЁїBOC=1ЃК3ЃЎ
гкЕуCЃЌЖЅЕуЮЊPЃЌДЫХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=1ЃЌЧвSЁїAOCЃКSЁїBOC=1ЃК3ЃЎ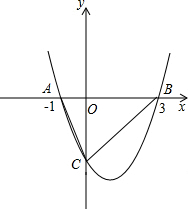 НтЃКЃЈ1ЃЉЁпSЁїAOCЃКSЁїBOC=1ЃК3ЃЌ
НтЃКЃЈ1ЃЉЁпSЁїAOCЃКSЁїBOC=1ЃК3ЃЌ =1ЃЌ
=1ЃЌ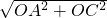 =
=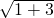 =
= ЃЌ
ЃЌ ЁС
ЁС =
= ЃЎ
ЃЎ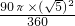 =
= ІаЃЛ
ІаЃЛ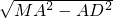 =1ЃЌ
=1ЃЌ ЃЎ
ЃЎ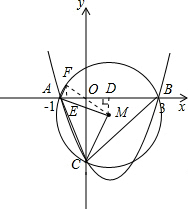
 ЃЛ
ЃЛ ЪБЃЌЁїABCЪЧЖлНЧШ§НЧаЮЃЎ
ЪБЃЌЁїABCЪЧЖлНЧШ§НЧаЮЃЎ ЃЛ
ЃЛ ЃЎ
ЃЎ Лђ
Лђ ЪБЃЌЁїABCЪЧЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїABCЪЧЕШбќШ§НЧаЮЃЎ

 ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 3 | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ACB=90ЖШЃЎ
ACB=90ЖШЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
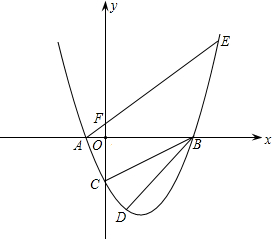 ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ-2ЃЉЃЌЧвЁЯACB=90ЖШЃЎ
ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ-2ЃЉЃЌЧвЁЯACB=90ЖШЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
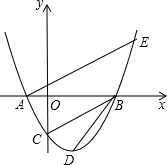
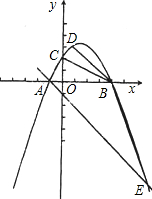 ЩшХзЮяЯпy=ax2+bx+cгыxжсНЛгкСНИіВЛЭЌЕФЕуAЃЈ-lЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ2ЃЉЃЎ
ЩшХзЮяЯпy=ax2+bx+cгыxжсНЛгкСНИіВЛЭЌЕФЕуAЃЈ-lЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ2ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 1 | 2 |
 m2-mb+nЃЉЃЌЦфжа aЃЌbЃЌcЃЌmЃЌnЮЊЪЕЪ§ЃЌЧвaЃЌmВЛЮЊ0ЃЎ
m2-mb+nЃЉЃЌЦфжа aЃЌbЃЌcЃЌmЃЌnЮЊЪЕЪ§ЃЌЧвaЃЌmВЛЮЊ0ЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com